ericpuwang

线性表

总结:

1. 线性表的逻辑结构特性是指数据元素之间存在着线性关系
2. 对于顺序表，元素存储的相邻位置反应出其逻辑上的线性关系，可借助数组来表示。给定数组的下标，便可以存取相应的元素，可称为随机存储结构。
3. 链表由一系列不必在内存中相连的结构组成。 每一个结构均含有表元素和指向包含该元素后继元的结构的指针。

顺序表和链表的比较

		顺序表	链表
空间	存储空间	预先分配，会导致空间闲置或溢出现象	动态分配，不会出现存储空间闲置或溢出现象
	存储密度	不用为表示结点间的逻辑关系而增加额外的存储开销，存储密度等于1	需要借助指针来体现元素间的逻辑关系，存储密度小于1
时间	存取元素	随机存取，按位置访问元素的时间复杂度为O(1)	顺序存储，按位置访问元素时间复杂度为O(n)
	插入、删除	平均移动约表中一半元素，时间复杂度为O(n)	不需要移动元素，确定插入、删除位置后，时间复杂度为O(1)
使用情况		表长变化不大，且能事先确定变化的范围 很少进行插入或者删除操作，经常按元素位置序号访问数据元素	长度变化较大 频繁进行插入和删除操作

单链表、循环链表和双向链表的比较

	查找表头结点	查找表尾结点	查找结点*p的前驱结点
带头结点的单链表L	L->next 时间复杂度O(1)	从L->next依次向后遍历 时间复杂度O(n)	通过p->next无法找到其前驱
带头结点仅设头指针L的循环单链表	L->next 时间复杂度O(1)	从L->next依次向后遍历 时间复杂度O(n)	通过p->next找到其前驱 时间复杂度O(n)
带头结点仅设尾指针R的循环单链表	R->next 时间复杂度O(1)	R 时间复杂度O(1)	通过p->next找到其前驱 时间复杂度O(n)
带头结点的双向循环链表L	L->next 时间复杂度O(1)	L->prior 时间复杂度O(1)	p->prior 时间复杂度O(1)

链表基础操作

结构体定义

typedef struct Node* PtrNode;
typedef struct Node Node;
struct Node {
    PtrNode next;
    int value;
}

链表是否为空

int isEmpty(PtrNode head)
{
    return head == NULL;
}

查找链表中元素为x的结点

PtrNode Find(PtrNode head, int x) {
    PtrNode p;
    if (head == NULL) {
        return NULL;
    }
    p = head->next;
    while (p!=NULL && p->value != x) {
        p = p->next;
    }
    return p;
}

删除链表中元素为x的结点

PtrNode Delete(PtrNode head, int x) {
    if (head == NULL) {
        return head;
    }

    PtrNode dummyHead = (PtrNode)malloc(sizeof(Node));
    dummyHead->next = head;

    PtrNode cur = dummyHead;
    while (cur->next!=NULL) {
        if (cur->next->value == x) {
            PtrNode tmp = cur->next;
            cur->next = tmp->next;
            free(tmp);
            break;
        }
        cur = cur->next;
    }
    return dummyHead->next;
}

链表中指定位置插入元素x

void Insert(PtrNode head, int index, int x) {
    PtrNode cur = head;
    // 获取到指定位置的上一个结点
    while (cur!=NULL&&index!=1) {
        cur=cur->next;
        index--;
    }
    if (cur == NULL) {
        return;
    }

    PtrNode node = (PtrNode)malloc(sizeof(Node));
    node->value = x;

    node->next = cur->next;
    cur->next = node;
    return;
}

打印链表

void Print(PtrNode head) {
    if (head == NULL) {
        return;
    }
    PtrNode cur = head;
    while (cur != NULL) {
        printf("%d->", cur->value);
        cur = cur->next;
    }
    printf("NULL\n");
}

链表的应用

多项式相加和相乘

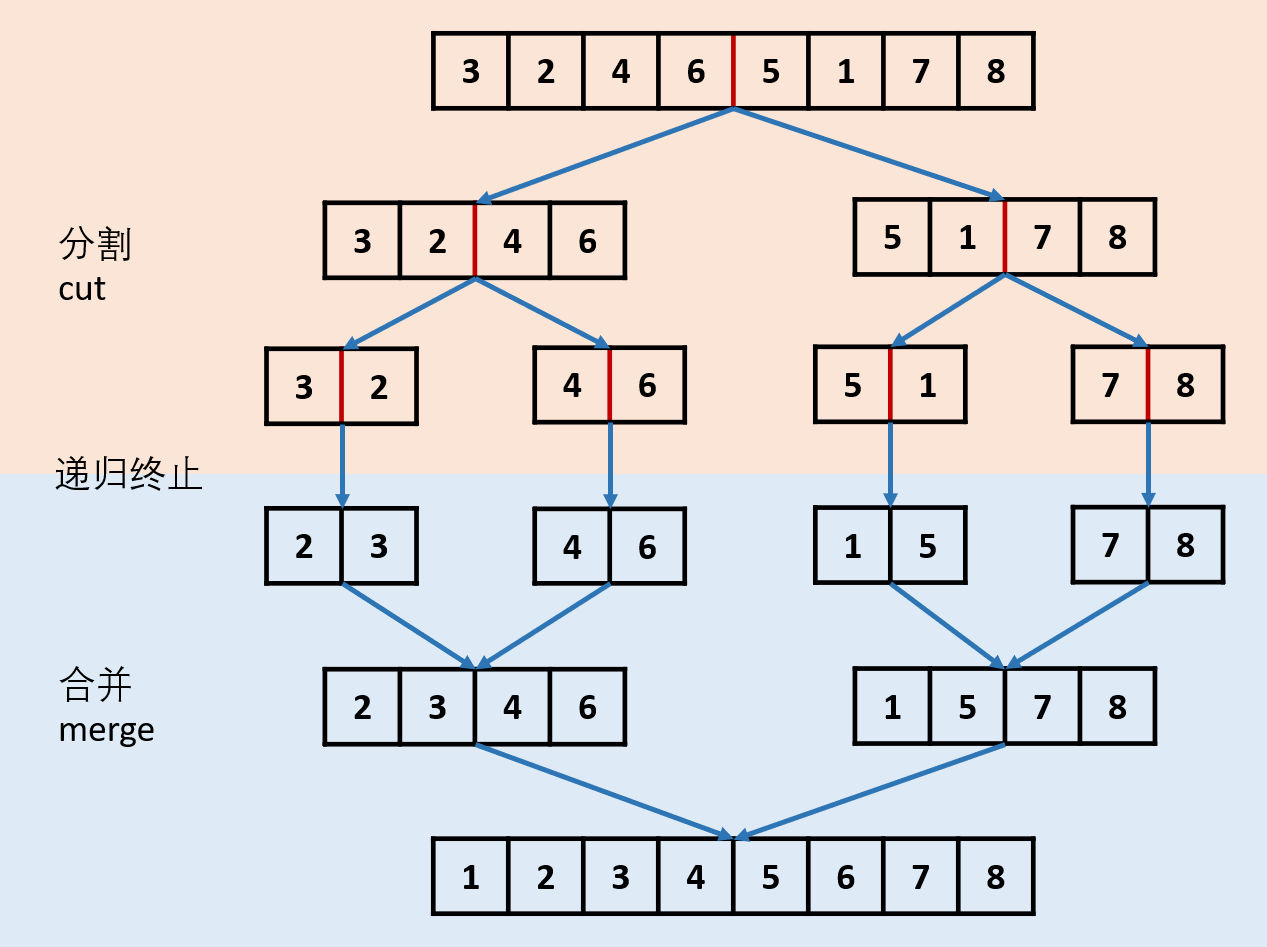
通过递归实现链表归并排序

• 分割 cut 环节：找到当前链表中点，并从中点将链表断开（以便在下次递归cut时，链表拥有正确的边界）
  • 使用fast, slow快慢指针，奇数个结点找到中点，偶数个结点找到中心左边的结点
  • 找到中点slow结点后，执行slow.next=None将链表切断
  • 递归分割时，输入当前链表左端点head和中心结点slow的下一个结点tmp（因为链表是从slow切断的）
  • cut 递归终止条件，当head.next=None时，说明只有一个结点了，直接返回此结点
• 合并 merge 环节：将两个有序链表合并，转化成一个有序链表
  • 双指针法合并，建立辅助PtrNode dummyHead作为头部
  • 设置两指针shadowHeadA，shadowHeadB分别指向两指针头部，比较两指针处结点值大小，由小到大加入合并链表头部，指针交替前进，直至添加完两个链表
  • 返回辅助PtrNode dummyHead作为头部的下个结点dummyHead->next
  • 时间复杂度O(m+n), m, n分别是两个链表的长度

#include<stdio.h>
#include<stdlib.h>

typedef struct Node Polynomial;
typedef struct Node* PtrNode;
struct Node {
    PtrNode next;
    double coefficient; // 系数
    int exponent; // 指数
};

void Print(PtrNode head) {
    if (head == NULL) {
        return;
    }
    PtrNode cur = head;

    int first = 0;
    printf("表达式:\t");
    while (cur != NULL) {
        if (cur->coefficient > 0 && first) {
            printf("+");
        }
        if (cur->exponent == 0) {
            printf("%d", cur->exponent);
        } else if (cur->exponent == 1) {
            printf("%dx", cur->exponent);
        } else {
            printf("%lgx^%d", cur->coefficient, cur->exponent);
        }
        cur = cur->next;
        first = 1;
    }
    printf("\n");
}

// Merge 合并两个有序链表
PtrNode Merge(PtrNode headA, PtrNode headB) {
    PtrNode dummyHead = (PtrNode) malloc(sizeof(Polynomial));
    PtrNode cur = dummyHead;
    PtrNode shadowHeadA = headA;
    PtrNode shadowHeadB = headB;

    while (shadowHeadA != NULL && shadowHeadB != NULL) {
        if (shadowHeadA->exponent <= shadowHeadB->exponent)
        {
            cur->next = shadowHeadA;
            shadowHeadA = shadowHeadA->next;
        } else {
            cur->next = shadowHeadB;
            shadowHeadB = shadowHeadB->next;
        }
        cur = cur->next;
    }
    if (shadowHeadA != NULL) {
        cur->next = shadowHeadA;
    }
    if (shadowHeadB != NULL) {
        cur->next = shadowHeadB;
    }
    return dummyHead->next;
}

// Sort 按指数降序排序
// 二分法归并排序(快慢指针)
PtrNode Sort(PtrNode head, PtrNode tail) {
    if (head == NULL) {
        return head;
    }
    if (head->next == tail) {
        head->next = NULL;
        return head;
    }

    PtrNode fast = head;
    PtrNode slow = head;
    while (fast != tail) {
        fast = fast->next;
        slow = slow->next;
        if (fast != tail) {
            fast = fast->next;
        }
    }
    return Merge(Sort(head, slow), Sort(slow, tail));
}

// CreatePolynomial 创建多项式
PtrNode CreatePolynomial(int length) {
    double coefficient;
    int exponent;

    PtrNode dummyHead = (PtrNode)malloc(sizeof(Polynomial));
    PtrNode cur = dummyHead;

    while (length--) {
        PtrNode node = (PtrNode)malloc(sizeof(Polynomial));
        scanf("%lg %d", &coefficient, &exponent);
        node->coefficient = coefficient;
        node->exponent = exponent;

        cur->next = node;
        cur = node;
    }
    return dummyHead->next;
}

// Add 多项式相加
PtrNode Add(PtrNode polynomialLeft, PtrNode polynomialRight) {
    PtrNode shadowPolynomialLeft = Sort(polynomialLeft, NULL);
    PtrNode shadowPolynomialRight = Sort(polynomialRight, NULL);

    if (polynomialLeft == NULL) {
        return polynomialRight;
    }
    if (polynomialRight == NULL) {
        return polynomialLeft;
    }

    PtrNode dummyHead = (PtrNode)malloc(sizeof(Polynomial));
    PtrNode cur = dummyHead;

    while (shadowPolynomialLeft->exponent<shadowPolynomialRight->exponent)
    {
        cur->next = shadowPolynomialLeft;
        cur = cur->next;
        shadowPolynomialLeft = shadowPolynomialLeft->next;
    }
    while (shadowPolynomialLeft!=NULL && shadowPolynomialRight!=NULL)
    {
        if (shadowPolynomialLeft->exponent == shadowPolynomialRight->exponent) {
            PtrNode node = (PtrNode)malloc(sizeof(Polynomial));
            node->exponent = shadowPolynomialLeft->exponent;
            node->coefficient = shadowPolynomialLeft->coefficient+shadowPolynomialRight->coefficient;
            cur->next = node;
            shadowPolynomialRight = shadowPolynomialRight->next;
            shadowPolynomialLeft = shadowPolynomialLeft->next;
        } else if (shadowPolynomialLeft->exponent < shadowPolynomialRight->exponent) {
            cur->next = shadowPolynomialLeft;
            shadowPolynomialLeft = shadowPolynomialLeft->next;
        } else {
            cur->next = shadowPolynomialRight;
            shadowPolynomialRight = shadowPolynomialRight->next;
        }
        cur = cur->next;
    }
    if (shadowPolynomialLeft != NULL) {
        cur->next = shadowPolynomialLeft;
    }
    if (shadowPolynomialRight != NULL) {
        cur->next = shadowPolynomialRight;
    }
    return dummyHead->next;
}

// Multi 多项式相乘
PtrNode Multi(PtrNode polynomialLeft, PtrNode polynomialRight) {
    if (polynomialLeft == NULL || polynomialRight == NULL) {
        return NULL;
    }

    PtrNode dummyHead = (PtrNode)malloc(sizeof(Polynomial));
    dummyHead->next = NULL;

    PtrNode shadowPolynomialLeft = Sort(polynomialLeft, NULL);
    PtrNode shadowPolynomialRight = Sort(polynomialRight, NULL);
    while(shadowPolynomialLeft != NULL)
    {
        PtrNode result = (PtrNode)malloc(sizeof(Polynomial));
        PtrNode cur = result;
        PtrNode p = shadowPolynomialRight;
        while (p != NULL)
        {
            PtrNode node = (PtrNode)malloc(sizeof(Polynomial));
            // 系数相乘
            node->coefficient = shadowPolynomialLeft->coefficient * p->coefficient;
            // 指数相加
            node->exponent = shadowPolynomialLeft->exponent + p->exponent;
            cur->next = node;

            cur = cur->next;
            p = p->next;
        }
        cur->next = NULL;
        dummyHead->next = Add(dummyHead->next, result->next);
        shadowPolynomialLeft = shadowPolynomialLeft->next;
    }
    return dummyHead->next;
}

int main() {
    int numberOfTerm;
    printf("请输入多项式的项数:\n");
    scanf("%d", &numberOfTerm);
    PtrNode polynomialLeft = CreatePolynomial(numberOfTerm);
    Print(polynomialLeft);

    printf("请输入多项式的项数:\n");
    scanf("%d", &numberOfTerm);
    PtrNode polynomialRight = CreatePolynomial(numberOfTerm);
    Print(polynomialRight);

    printf("多项式相加\n");
    PtrNode result = Add(polynomialLeft, polynomialRight);
    Print(result);

    printf("多项式相乘\n");
    result = Multi(polynomialLeft, polynomialRight);
    Print(result);

    return 0;
}

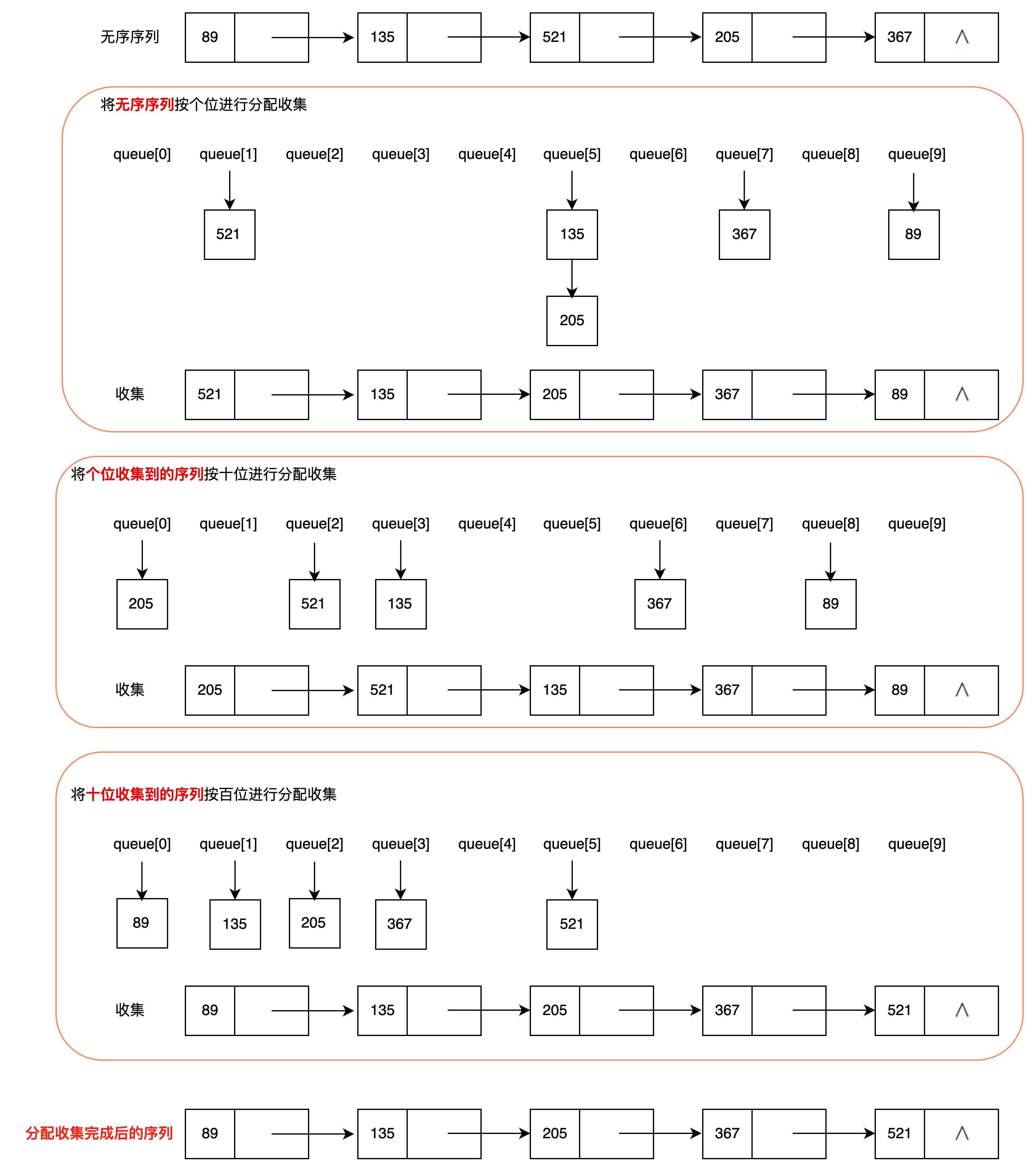
基数排序

• 以静态链表存储待排记录，并令表头指针指向第一个记录
• “分配” 时，按当前“关键字位”所取值，将记录分配到不同的 “链队列” 中，每个队列中记录的 “关键字位” 相同
• “收集”时，按当前关键字位取值从小到大将各队列首尾相链成一个链表
• 对每个关键字位均重复 2 和 3 两步

// 基数排序
#include<stdio.h>
#include<stdlib.h>

typedef struct Node {
    int value;
    struct Node* next;
} Node;

// ShowNode 打印链表
void ShowNode(Node* head) {
    Node* p = head;
    while(p != NULL)
    {
        printf("%d\t", p->value);
        p = p->next;
    }
}

// CreateNode 创建链表
Node* CreateNode() {
    Node* head = (Node*)malloc(sizeof(Node));
    Node* cur = head;
    int length = 0;
    printf("请输入待排序链表的长度:");
    while(length<=0) {
        scanf("%d", &length);
        if (length <= 0) {
            printf("请输入大于零的整数\n");
        }
    }
    printf("请输入%d个整数\n", length);
    for (int i=0; i<length; i++) {
        Node* node = (Node*)malloc(sizeof(Node));
        scanf("%d", &node->value);
        cur->next = node;
        cur = cur->next;
    }
    cur->next = NULL;

    return head->next;
}

// Length 返回链表长度
int Length(Node* head)
{
    int length = 0;
    Node* cur = head;
    while(cur!=NULL)
    {
        length++;
        cur = cur->next;
    }
    return length;
}

// GetNumInPos 返回整数num在pos位的数
int GetNumInPos(int num, int pos)
{
    int temp = 1;
    for (int i=1;i<pos;i++) {
        temp *= 10;
    }
    return (num/temp)%10;
}

// GetDigitOfNum 返回整数num有多少位
int GetDigitOfNum(int num)
{
    int n = 1, temp = 10;
    while (temp <= num) {
        n++;
        temp*=10;
    }
    return n;
}

// GetMaxDigit 返回链表中最大数有几位数
int GetMaxDigit(Node* head) {
    Node* cur = head;
    int n, max;
    while(cur!=NULL) {
        n = GetDigitOfNum(cur->value);
        if (n > max) {
            max = n;
        }
        cur = cur->next;
    }
    return max;
}

// RadixSort 基数排序
void RadixSort(Node* head) {
    int nodeLength = Length(head);
    int index[10][nodeLength]; // 二维数组分类, 从上到下0-9, 对应数字的每行可保存nodeLength个数
    int count[10]; // 用数组记录被分配基数个数
    int maxDigit = GetMaxDigit(head);

    for (int pos = 0; pos < maxDigit; pos++)
    {
        Node* p = head;
        for (int i = 0; i < 10; i++)
        {
            count[i] = 0;
        }
        while (p != NULL)
        {
            int n = GetNumInPos(p->value, pos+1);
            index[n][count[n]] = p->value;
            count[n]++;
            p = p->next;
        }

        Node* l = head;
        for (int i = 0; i < 10;i++)
        {
            for (int j=0; j < count[i]; j++)
            {
                l->value = index[i][j];
                l = l->next;
            }
        }
        printf("第%d次排序:\n", pos+1);
        ShowNode(head);
        printf("\n");
    }
}

int main()
{
    Node* head = CreateNode();
    printf("已经创建单链表:\n");
    ShowNode(head);
    printf("\n");
    RadixSort(head);
    printf("最终排序结果:\n");
    ShowNode(head);
    return 0;
}