ericpuwang

图

子图: 假设有两个图G=(V,E),G’=(V’,E’), 若V’是V的子集且E’是E的子集，则称G’是G的子集

无向完全图和有向完全图: 对于无向图，若具有n(n-1)/2条边，则称为无向完全图。对于有向图，若具有n(n-1)条弧，则称为有向完全图

稀疏图和稠密图: 有很少条边或弧(如 $e<nlog_2n$ )的图称为稀疏图，反之称为稠密图

权和网：在实际应用中，每条边可以标上具有某种含义的数值，该数值称为该边上的权。这些权可以表示从一个顶点到另一个顶点的距离，这种带权的图通常称为网

邻接点：对于无向图G，如果图的边 $(v,v’) \in E$ ，则称顶点v和v’互为邻接点，即v和v’相邻接。边(v,v’)依附于顶点v和v’，或者说边(v,v’)与顶点v和v’相关联

度、入度和出度: 顶点v的度是指和v相关联的边的数目。对于有向图，顶点v的度分为入度和出度。入度是以顶点v为头的弧的数目, 出度是以顶点v为尾的弧的数目

路径和路径长度: 在无向图中，从顶点v到顶点v’的路径是一个顶点序列( $v=v_{i,0},v_{i,1},\cdots,v_{i,m}=v’$ )，其中( $v_{i,j-1},v_{i,j} \in E, 1 \leq j \leq m$ )。在有向图中，路径也是有向的，顶点序列应满足 $<v_{i,j-1},v_{i,j}> \in E, 1 \leq j \leq m$ 。路径长度是一条路径上经过的边或弧的数目

回路或环：第一个顶点和最后一个顶底相同的路径称为回路或环

简单路径、简单回路或简单环: 序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环

连通、连通图和连通分量: 在无向图G中，如果从顶点v到顶点v’有路径，则称v和v’是连通的。如果对于图中任意两个顶点 $v_i, v_j \in V, v_i$ 和 $v_j$ 都是连通的，则称G为连通图。所谓连通分量，指的是无向图中极大连通子图

强连通图和强连通分量: 在有向图G中，如果对于每一对 $v_i,v_j \in V, v_i \ne v_j$ , 从 $v_i$ 到 $v_j$ 和从 $v_j$ 到 $v_i$ 都存在路径，则称G是强连通图。有向图中的极大连通子图称为有向图的强连通分量

连通图的生成树: 一个极小连通子图，它含有图中全部顶点，但只有足以构成一棵树的n-1条边，这样的连通子图称为连通图的生成树

有向树和生成森林: 有一个顶点的入度为0，其余顶点的入度均为1的有向图称为有向树，一个有向图的生成森林是有若干棵有向树组成

图的存储结构

邻接矩阵

优点

便于判断两个顶点之间是否有边,即根据A[i][j]=0或1来判断
便于计算各顶点的度。对于无向图，邻接矩阵第i行元素之和即为顶底i的度；对于有向图，第i行元素的和就是顶点i的出度，第i列元素的和为顶点i的入度

缺点

不便于增加和删除顶点
不便于统计边的数目，需要扫描邻接矩阵所有元素才能统计完毕。时间复杂度为 $O(n^2)$
空间复杂度高，复杂度为 $O(n^2)$

用二维数组来表示元素之间的关系

邻接矩阵是表示顶点之间相邻关系的矩阵。设G(V,E)是具有n个顶点的图，则G的邻接矩阵是具有如下性质的n阶方阵

\[A[i][j] = \begin{cases} 1 \qquad <v_i, v_j> \text{或} (v_i, v_j) \in E \\ 0 \qquad \text{反之} \end{cases}\]

示例:

\[G_{1,arcs} = \begin{bmatrix} 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix}\]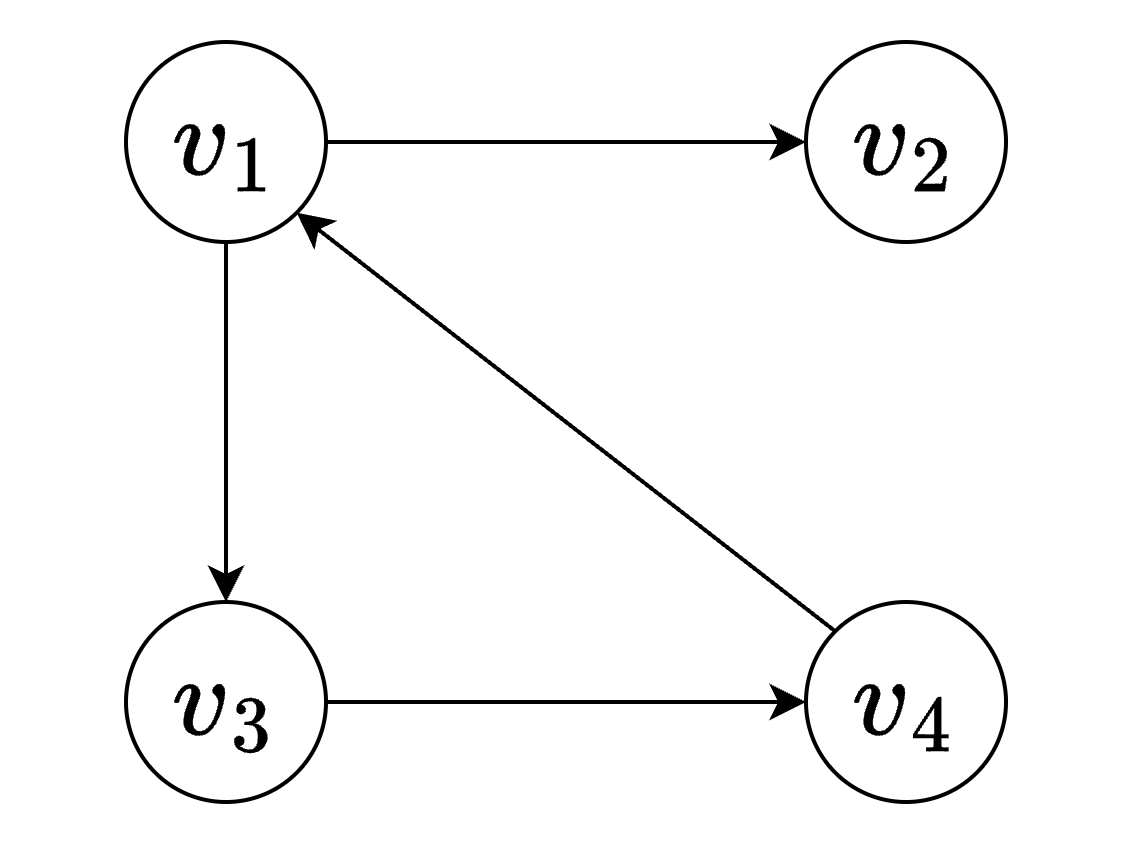

邻接矩阵_有向图.png 若G是网 ，则邻接矩阵可以定义为

\[A[i][j] = \begin{cases} w_{i,j} \qquad \text{若}<v_i, v_j> \text{或} (v_i, v_j) \in E, \text{表示边上的权值} \\ \infty \end{cases}\]

示例:

\[\begin{bmatrix} \infty & 5 & \infty & 7 & \infty & \infty \\ \infty & \infty & 4 & \infty & \infty & \infty \\ 8 & \infty & \infty & \infty & \infty & 9 \\ \infty & \infty & 5 & \infty & \infty & 6 \\ \infty & \infty & \infty & 5 & \infty & \infty \\ 3 & \infty & \infty & \infty & 1 & \infty \\ \end{bmatrix}\]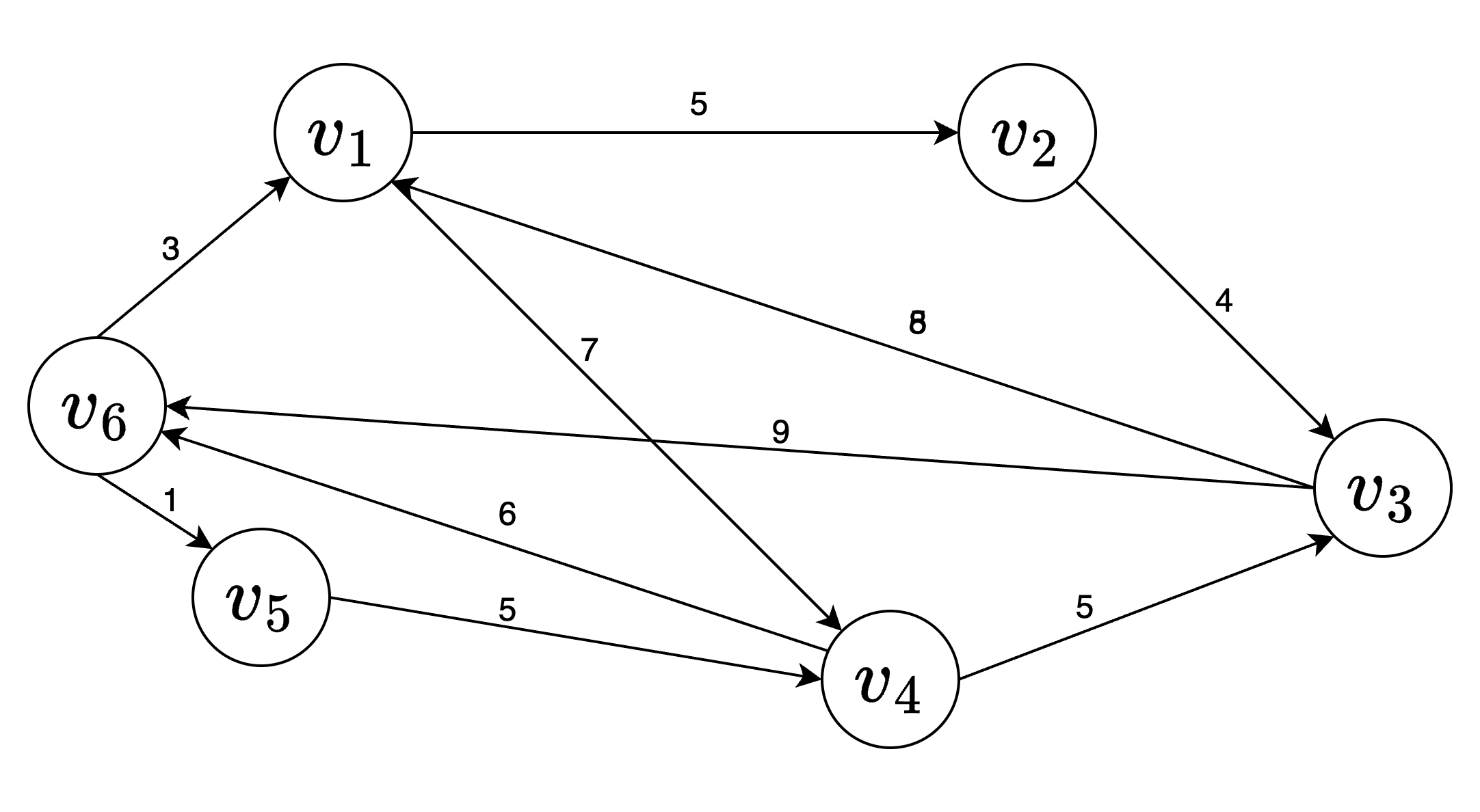

邻接矩阵_网.png 创建无向网 时间复杂度 $O(n^2)$

// 图的邻接矩阵存储表示
#define MaxInt 32767 // 表示极大值∞
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct
{
    VerTexType vexs[MVNum]; // 顶点表
    ArcType arcs[MVNum][MVNum]; // 邻接矩阵
    int vexnum, arcnum; // 图的当前顶点数和边数
}AMGraph;

// 确定顶点v的在图中的位置
int LocateVex(AMGraph *g, VerTexType v)
{
    for (int i = 0; i < g->vexnum; i++)
    {
        if (g->vexs[i] == v)
        {
            return i;
        }
    }
    return -1;
}

// 采用邻接矩阵表示法创建无向网
// 1. 输入总顶点数和总边数
// 2. 依次输入点的信息存储顶点表
// 3. 初始化邻接矩阵，使每个权值初始化为极大值
// 4. 构造邻接矩阵，依次输入每条边依附的顶点和其权值，确定两个顶点在图中的位置之后，使相应边
//    赋予相应的权值，同时使其对称边赋予相同的权值
int CreateUDN(AMGraph *g)
{
    // 输入总顶点数，总边数
    scanf("%d%d", &g->vexnum, &g->arcnum);
    // 依次输入点的信息
    for (int i = 0; i < g->vexnum; ++i)
    {
        scanf("%c", &g->vexs[i]);
    }
    // 初始化邻接矩阵
    for (int i = 0; i < g->vexnum; i++)
    {
        for (int j = 0; j < g->vexnum; j++)
        {
            g->arcs[i][j] = MaxInt;
        }
    }
    // 构造邻接矩阵
    VerTexType v1, v2;
    ArcType w;
    for (int k = 0; k < g->arcnum; k++)
    {
        scanf("%c%c%d", &v1,&v2,&w);
        int i = LocateVex(g, v1);
        int j = LocateVex(g, v2);
        if (i == -1 || j == -1) {
            return -1;
        }
        g->arcs[i][j] = w;
    }
    return 0;
}

创建无向图

针对上述代码，做如下改动即可:

初始化邻接矩阵时，将边的权值初始化为0
构造邻接矩阵时，将权值w改为常量1即可

邻接表

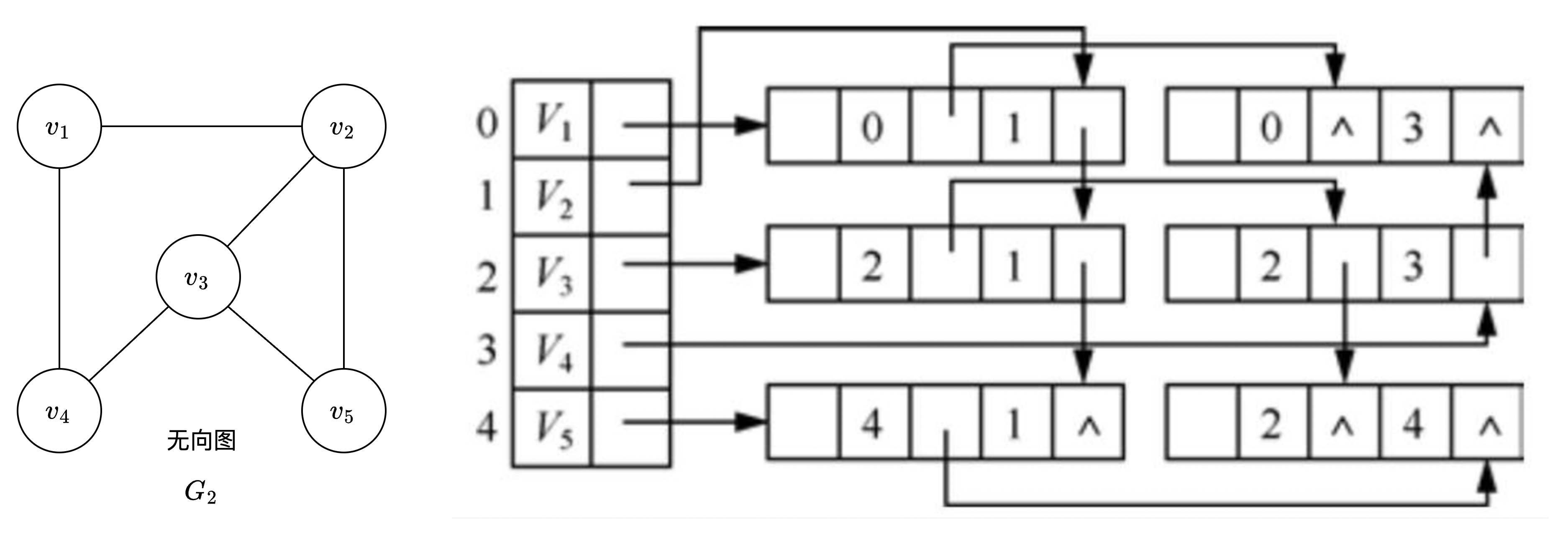
邻接表是图的一种链式存储结构。在邻接表中，对图中每个顶点 $v_i$ 建立一个单链表，把与 $v_i$ 相邻接的顶点放在这个链表中。邻接表中每个单链表的第一个结点存放有关顶点的信息，把这一结点看成链表的表头，其余结点存放有关边的信息，这样邻接表便由两部分组成：表头结点表和边表

表头结点表：由所有表头结点以顺序结构的形式存储，以便可以随机访问任一顶点的边链表。表头结点包括数据域和链域（数据域用于存储顶点 $v_i$ 的名称和其他有关信息；链域用于指向链表中第一个结点即与顶点 $v_i$ 邻接的第一个邻接点）
边表：由表示图中顶点间关系的2n个边链表组成。边链表中边结点包括邻接点域(adjvex)、数据域(info)和邻域(nextarc)三部分
- 邻接点域指示与顶点 $v_i$ 相邻的点在图中的位置
- 数据域存储和边相关的信息，如权值等
- 链域指示与顶点 $v_i$ 邻接的下一条边的结点

邻接表_表头结点和边结点.png

无向图的邻接表中，顶点 $v_i$ 的度恰为第i个链表中的结点数
在有向图中，第i个链表的结点数只是顶点 $v_i$ 的出度；为求入度，必须遍历整个邻接表
在所有链表中，其邻接点域的值为i的结点个数是顶点i的入度

逆邻接表 对每个顶点 $v_i$ 建立一个链接所有进入 $v_i$ 的边的表

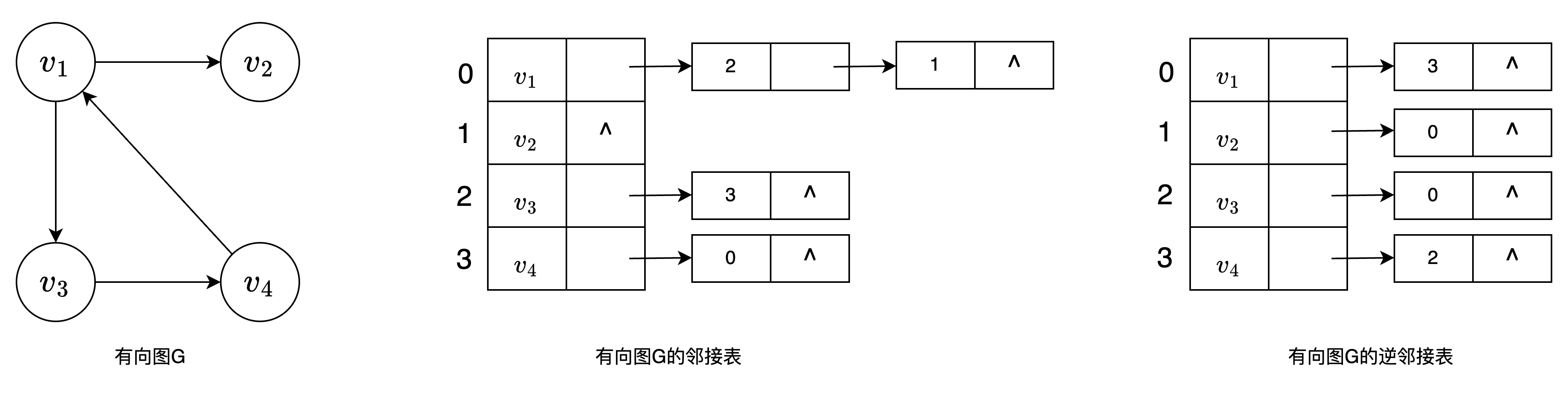
邻接表和逆邻接表.png

#include<stdio.h>
#include<stdlib.h>
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct OtherInfo {

}OtherInfo;

typedef struct ArcNode {
    int adjvex; // 该边所指向的顶点的位置
    struct ArcNode *nextarc; // 指向下一条边的指针
    OtherInfo into; // 和边相关的信息;
}ArcNode;

typedef struct VNode {
    VerTexType data;
    ArcNode *firstarc; // 指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum];

typedef struct ALGraph {
    AdjList vertices;
    int vexnum, arcnum; // 图的当前顶点数和边数
}ALGraph;

// 确定顶点v的在图中的位置
int LocateVex(ALGraph *g, VerTexType v)
{
    for (int i = 0; i < g->vexnum; i++)
    {
        if (g->vertices[i].data == v)
        {
            return i;
        }
    }
    return -1;
}

// 采用邻接表表示法创建无向图
// 1. 输入总顶点数和总边数
// 2. 依次输入点的信息存储顶点表，使每个表头结点的指针域初始化为NULL
// 3. 创建邻接表，依次输入每条边依附的两个顶点，确定这两个顶点的序号i和j后，将此边结点分别插入相应边链表的头部
int CreateUDG(ALGraph *g)
{
    scanf("%d%d", &g->vexnum, &g->arcnum);
    for (int i = 0; i < g->vexnum; i++)
    {
        scanf("%c", &g->vertices[i].data);
        g->vertices[i].firstarc = NULL;
    }
    for (int k = 0; k < g->arcnum; k++)
    {
        VerTexType v1, v2;
        scanf("%c%c", &v1, &v2);
        // 确定v1,v2在g中的位置，即顶点在g->vertices中的序号
        int i = LocateVex(g, v1);
        int j = LocateVex(g, v2);

        if (i == -1 || j == -1) {
            return -1;
        }

        // 将新结点p1插入到vi的边表头部
        ArcNode *p1 = (ArcNode*)malloc(sizeof(ArcNode));
        p1->adjvex = j;
        p1->nextarc = g->vertices[i].firstarc;
        g->vertices[i].firstarc = p1;

        // 将新结点p2插入到vj的边表头部
        ArcNode *p2 = (ArcNode*)malloc(sizeof(ArcNode));
        p2->adjvex = i;
        p2->nextarc = g->vertices[j].firstarc;
        g->vertices[j].firstarc = p2;
    }
    return 0;
}

建立有向图的邻接表与此类似，只是更加简单，每读入一个顶点对序号<i, j>，仅需生成一个邻接点序号为j的边表结点，并将其插入到 $v_i$ 的边链表头部即可。若要创建网的邻接表，可以将边的权值存储在info域中

优缺点

优点

便于增加和删除顶点
便于统计边的数目，按照顶点表顺序扫描所有边表可得到边的数目，其时间复杂度为 O(n+e)
空间效率高。对于一个具有n个顶点e条边的图G，若G是无向图，则其在邻接表表示中有 n 个顶点和 2e 个边表结点；若G是有向图，则在它的邻接表或逆邻接表表示中有 n 个顶点和 e 个边表结点，因此邻接表或逆邻接表表示的空间复杂度为 O(n+e) ，适合表示稀疏图

缺点

不便于判断顶点之间是否有边，要判定 $v_i$ 和 $v_j$ 之间是否有边，就需要扫描第i个边表，时间复杂度O(n)
不便于计算有向图各个顶点的度。对于无向图，在邻接表表示中顶点 $v_i$ 的度是第i个边表中的结点个数。在有向图的邻接表中，第i个边表上的结点个数是顶点 $v_i$ 的出度，但求 $v_i$ 的入度比较困难，需要遍历各顶点的边表；若有向图采用逆邻接表表示，则与之相反，第i个边表上的结点个数是顶点 $v_i$ 的入度

邻接矩阵和邻接表的比较
比较项目存储结构		邻接矩阵		邻接表
比较项目存储结构		无向图	有向图	无向图	有向图
空间		邻接矩阵对称，可压缩至`n(n-1)/2`个单元	邻接矩阵不对称，存储`n²`个单元	存储`n+2e`个单元	存储`n+e`个单元
时间	求某个顶点v_i的度	扫描邻接矩阵中序号i对应的一行。`O(1)`	求出度: 扫描矩阵的一行。`O(n)` 求入度: 扫描矩阵的一列。`O(n)`	扫描v_i的边表。最坏情况`O(n)`	求出度: 扫描v_i的边表。最坏情况`O(n)` 求入度: 按顶点表顺序扫描所有边表。`O(n+e)`
	求边的数目	扫描邻接矩阵。`O(n²)`		按顶点表顺序扫描所有边表。`O(n+2e)`	按顶点表顺序扫描所有边表。`O(n+e)`
	判定边(v_i, v_j)是否存在	直接检查邻接矩阵A[i][j]元素的值。`O(1)`		扫描v_i的边表。最坏情况`O(n)`
使用情况		稠密图		稀疏图

十字链表

十字链表是 有向图 的另一个链式存储结构。可以看成是将有向图的邻接表和逆邻接表结合起来得到的一种链表。在十字链表中，对应于有向图中每一条弧有一个结点，对应于每个顶点也有一个结点，结点的结构如下图所示: 十字链表_结点.png

弧结点中

尾域(tailvex): 表示弧尾在图中的结点
头域(headvex): 表示弧头在图中的结点
链域(hlink): 表示指向弧头相同的下一条弧
链域(tlink): 表示指向弧尾相同的下一条弧
info域: 指向该弧的相关信息弧头相同的弧在同一链表上；弧尾相同的弧也在同一链表上。它们的头结点即为顶点结点。

顶点结点中

data域存储和顶点相关的信息，如顶点的名称等
firstin指向以该顶点为弧头的第一个弧结点
firstout指向以该顶点为弧尾的第一个弧结点

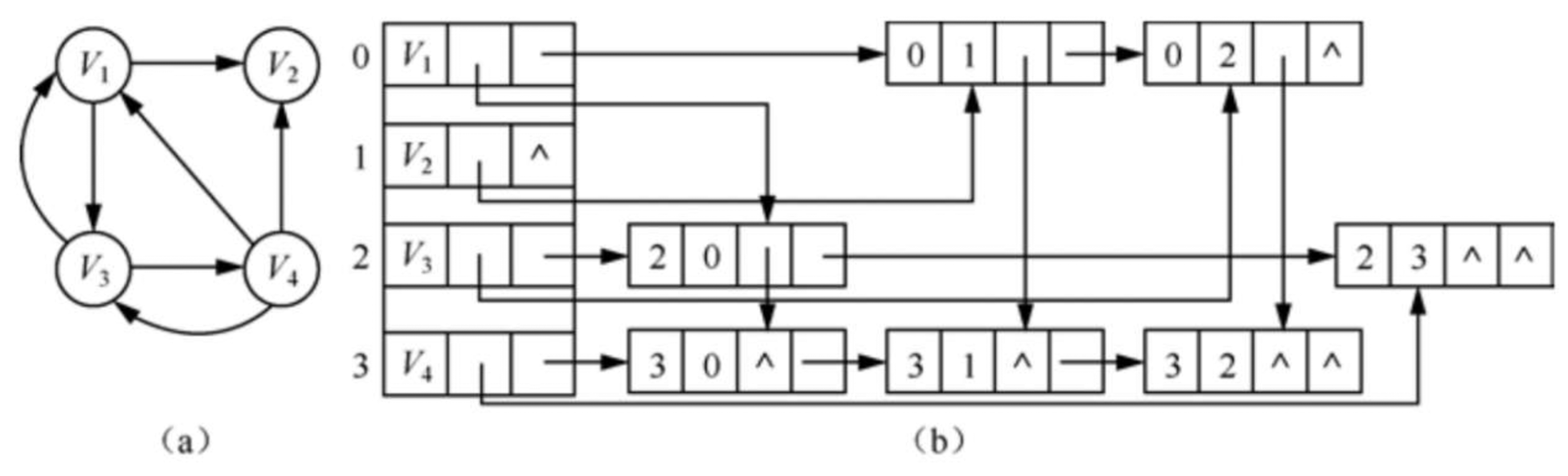有向图的十字链表.png 若将有向图的邻接矩阵看成稀疏矩阵的话，则十字链表也可以看成是邻接矩阵的链式存储结构，在图的十字链表中，弧结点所在的链表非循环链表，结点之间相对位置自然形成，不一定按照顶点序号有序，表头结点即顶点结点，它们之间不是链接，而是顺序存储。

#include<stdio.h>
#include<stdlib.h>

#define MAX_VERTEX_NUM  20
typedef char VertexType;

typedef struct InfoType {
}InfoType;

typedef struct ArcBox {
    int tailvex, headvex; // 该狐的尾和头顶点的位置
    struct ArcBox *hlink, *tlink; // 分别为狐头相同和狐尾相同的狐的链域
    InfoType *info; // 该狐相关信息的指针
}ArcBox;

typedef struct VexNode {
    VertexType data;
    ArcBox *firstin, *firstout; // 分别指向第一条入狐和出狐
}VexNode;

typedef struct OLGraph {
    VexNode xlist[MAX_VERTEX_NUM]; // 表头向量
    int vexnum, arcnum; // 有向图的当前顶点数和狐数
}OLGraph;

int Locate(OLGraph *g, VertexType x)
{
    for (int i = 0; i < g->vexnum; i++)
    {
        if (g->xlist[i].data == x)
        {
            return i;
        }
    }
    return -1;
}

int createGraph(OLGraph *g)
{
    printf("请输入图的顶点数和狐数\n");
    scanf("%d%d", &g->arcnum, &g->vexnum);

    printf("请依次输入每个顶点\n");
    for (int i = 0; i < g->vexnum; i++)
    {
        scanf("%c", &g->xlist[i].data);
        g->xlist[i].firstin = NULL;
        g->xlist[i].firstout = NULL;
    }

    printf("请依次输入每条狐的起点和终点\n");
    for (int k = 0; k < g->arcnum; k++)
    {
        VertexType x, y;
        scanf("%c%c", &x, &y);
        int i = Locate(g, x);
        int j = Locate(g, y);
        if (i == -1 || j == -1) {
            return -1;
        }

        // 创建结点
        ArcBox *node = (ArcBox*)malloc(sizeof(ArcBox));
        node->headvex = i;
        node->tailvex = j;

        // 将该结点添加到以i为起始结点的链表上
        node->hlink = g->xlist[i].firstin;
        g->xlist[i].firstin = node;
        // 将该结点添加到以j为尾结点的链表上
        node->tlink = g->xlist[i].firstout;
        g->xlist[i].firstout = node;
    }
    return 0;
}

邻接多重表

邻接多重表是 无向图 的另一种链式存储结构。虽然邻接表是无向图的一种很有效的存储结构，在邻接表中容易求得顶点和边得各种信息。但是在邻接表中每一条边 $(v_i,v_j)$ 有两个结点，分别在第i和第j个链表中，这给某些图得操作带来不便，而采用邻接多重表得无向图更为适宜解决这一类问题

在邻接多重表中，每一条边用一个结点表示，由如下所示得6个域组成:

mark标志域：标记该条边是否被搜索过
ivex和jvex：该边依附得两个顶点在图中得位置
ilink：指向下一条依附于顶点ivex的边
jlink：指向下一条依附于顶点jvex的边
info：指向和边相关的各种信息的指针域

每一个顶点也用一个结点表示，由如下所示2个域组成:

data：data域存储和顶点相关的信息
firstedge：firstedge域指示第一条依附于该顶点的边

邻接多重表.png 无向图的邻接多重表.png

#include<stdio.h>
#include<stdlib.h>

#define MAX_VERTEX_NUM  20
typedef enum{unvisited, visited} VisitIf;
typedef char VertexType;

typedef struct InfoType {
}InfoType;

typedef struct EBox {
    VisitIf mark; // 访问标记
    int ivex, jvex; // 该边依附的两个顶点的位置
    struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条边
    InfoType *info; // 该狐相关信息的指针
}EBox;

typedef struct VexBox {
    VertexType data;
    EBox *firstedge; // 指向第一条依附该顶点的边
}VexBox;

typedef struct AMLGraph {
    VexBox adjmulist[MAX_VERTEX_NUM];
    int vexnum, edgenum; // 无向图的当前顶点数和边数
}AMLGraph;

int Locate(AMLGraph *g, VertexType x)
{
    for (int i = 0; i < g->vexnum; i++)
    {
        if (g->adjmulist[i].data == x)
        {
            return i;
        }
    }
    return -1;
}

int createUDG(AMLGraph *g)
{
    printf("输入顶点数，边数\n");
    scanf("%d,%d,%d", &g->vexnum, &g->edgenum);

    printf("请输入顶点数\n");
    for(int i = 0; i < g->vexnum; i++)
    {
        scanf("%c", &g->adjmulist[i].data);
        g->adjmulist[i].firstedge = NULL;
    }

    printf("请依次输入每条狐的起点和终点\n");
    for (int k = 0; k < g->edgenum; k++)
    {
        VertexType x, y;
        scanf("%c%c", &x, &y);
        int i = Locate(g, x);
        int j = Locate(g, y);
        if (i == -1 || j == -1)
        {
            return -1;
        }

        EBox *box = (EBox *)malloc(sizeof(EBox));
        box->ivex = i;
        box->jvex = j;
        box->mark = unvisited;
        box->ilink = g->adjmulist[i].firstedge;
        box->jlink = g->adjmulist[j].firstedge;
        g->adjmulist[j].firstedge = box;
        g->adjmulist[i].firstedge = box;
    }
    return 0;
}

图的遍历

深度优先搜索

类似于树的先序遍历

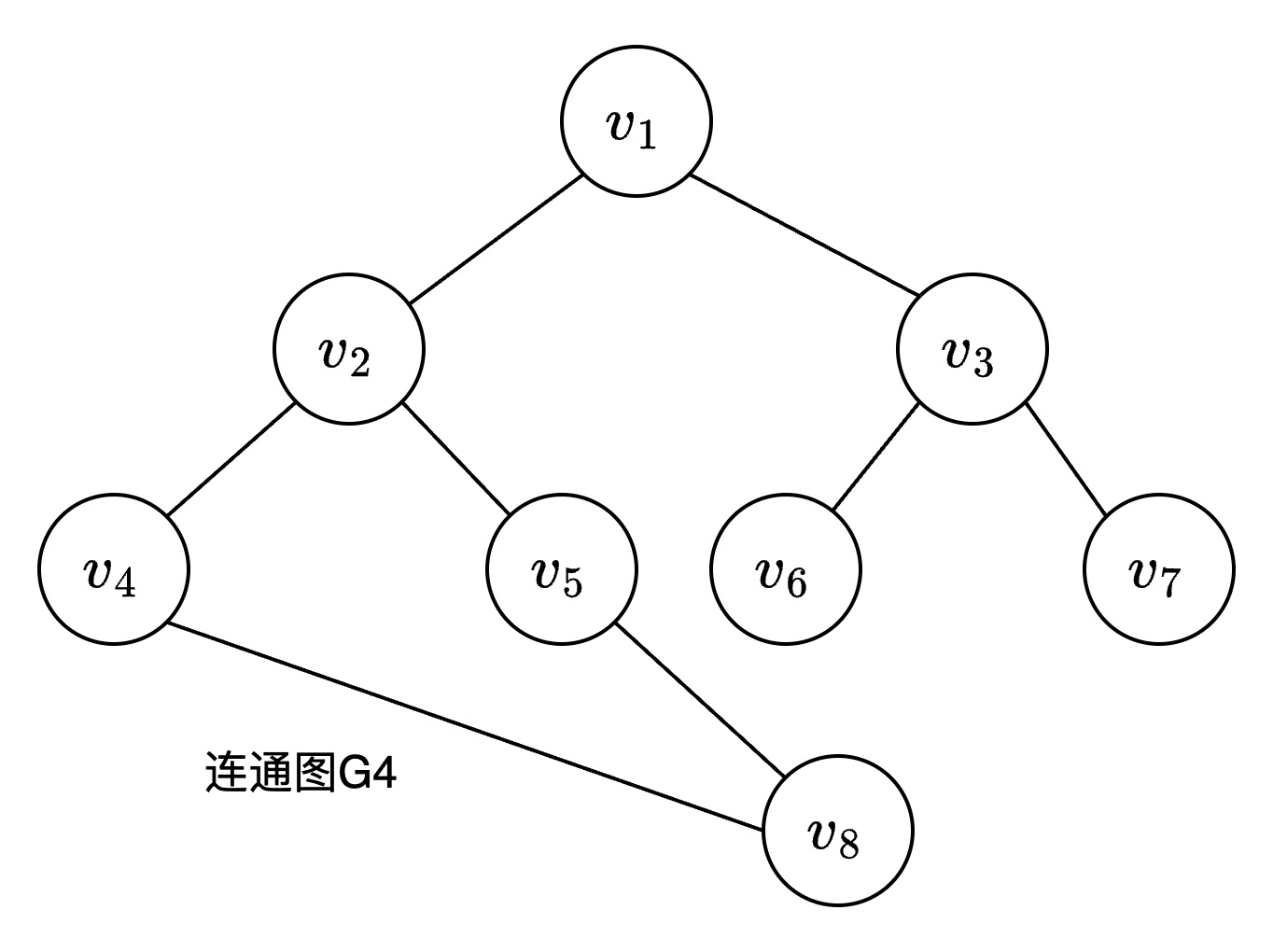连通图G4 对于一个连通图，深度优先搜索遍历的过程如下：

从图中某个顶点v出发，访问v
找出刚访问过的顶点的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点，重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止
返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点
重复步骤(2)和(3)，直至图中所有顶点都被访问过，搜索结束

对于连通图G4, 遍历路径 $v_1 -> v_2 -> v_4 -> v_8 -> v_5 -> v_3 -> v_6 -> v_7$

#include<stdio.h>
#include<stdlib.h>
#define MVNum 100 // 最大顶点数

typedef enum{unvisited, visited} VisitIf;
typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct OtherInfo {
}OtherInfo;

typedef struct ArcNode {
    int adjvex; // 该边所指向的顶点的位置
    struct ArcNode *nextarc; // 指向下一条边的指针
    OtherInfo into; // 和边相关的信息;
}ArcNode;

typedef struct VNode {
    VerTexType data;
    ArcNode *firstarc; // 指向第一条依附该顶点的边的指针
    VisitIf mark; // 访问标记
}VNode, AdjList[MVNum];

typedef struct ALGraph {
    AdjList vertices;
    int vexnum, arcnum; // 图的当前顶点数和边数
}ALGraph;

// 邻接表图的深度优先搜索
void ALGraphDFS(ALGraph *g, int v)
{
    printf("visited %d\n", v);
    g->vertices[v].mark = visited;
    ArcNode *p = g->vertices[v].firstarc;
    while (p != NULL)
    {
        if (g->vertices[p->adjvex].mark == unvisited)
        {
            ALGraphDFS(g, p->adjvex);
        }
        p = p->nextarc;
    }
}

void ALGraphDFSTraverse(ALGraph *g)
{
    for (int v = 0; v < g->vexnum; v++)
    {
        if (g->vertices[v].mark == unvisited)
        {
            ALGraphDFS(g, p->adjvex);
        }
    }
}

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 100

typedef enum{unvisited, visited} VisitIf;

typedef struct Node {
    int vertex;
    struct Node* next;
    VisitIf mark;
} Node;

typedef struct Graph {
    int numVertices;
    Node* adjLists[MAX_VERTICES];
} Graph;

// 创建图
Graph* createGraph(int vertices) {
    Graph* graph = malloc(sizeof(Graph));
    graph->numVertices = vertices;

    for (int i = 0; i < vertices; i++) {
        graph->adjLists[i] = NULL;
    }
    return graph;
}

// 创建节点
Node* createNode(int v) {
    Node* newNode = malloc(sizeof(Node));
    newNode->vertex = v;
    newNode->next = NULL;
    return newNode;
}

// 添加边
void addEdge(Graph* graph, int src, int dest) {
    Node* newNode = createNode(dest);
    newNode->next = graph->adjLists[src];
    graph->adjLists[src] = newNode;

    newNode = createNode(src);
    newNode->next = graph->adjLists[dest];
    graph->adjLists[dest] = newNode;
}

// 查找第一个邻接顶点
int FirstAdjVex(Graph* graph, int vertex) {
    Node* adjList = graph->adjLists[vertex];
    if (adjList != NULL) {
        return adjList->vertex; // 返回第一个邻接顶点
    }
    return -1; // 如果没有邻接顶点，返回-1
}

// 查找下一个邻接顶点
int NextAdjVex(Graph* graph, int vertex, int current) {
    Node* adjList = graph->adjLists[vertex];
    while (adjList != NULL) {
        if (adjList->vertex == current) {
            if (adjList->next != NULL) {
                return adjList->next->vertex; // 返回下一个邻接顶点
            } else {
                return -1; // 如果没有下一个邻接顶点，返回-1
            }
        }
        adjList = adjList->next;
    }
    return -1; // 如果没有找到当前顶点，返回-1
}

// 深度优先搜索
void DFS(Graph* graph, int vertex, int* visited) {
    visited[vertex] = 1; // 标记为已访问
    printf("Visited %d\n", vertex);

    int adjVertex = FirstAdjVex(graph, vertex);
    while (adjVertex != -1) {
        if (!visited[adjVertex]) {
            DFS(graph, adjVertex, visited);
        }
        adjVertex = NextAdjVex(graph, vertex, adjVertex);
    }
}

// 打印图
void printGraph(Graph* graph) {
    for (int v = 0; v < graph->numVertices; v++) {
        Node* temp = graph->adjLists[v];
        printf("Vertex %d: ", v);
        while (temp) {
            printf("%d -> ", temp->vertex);
            temp = temp->next;
        }
        printf("NULL\n");
    }
}

int main() {
    Graph* graph = createGraph(5);

    addEdge(graph, 0, 1);
    addEdge(graph, 0, 4);
    addEdge(graph, 1, 2);
    addEdge(graph, 1, 3);
    addEdge(graph, 1, 4);
    addEdge(graph, 2, 3);
    addEdge(graph, 3, 4);

    printGraph(graph);

    int visited[MAX_VERTICES] = {0}; // 访问标记数组
    printf("Depth First Search starting from vertex 0:\n");
    DFS(graph, 0, visited);

    return 0;
}

广度优先搜索

类似于树的按层序遍历

遍历过程如下:

从图中某个顶点v出发，访问v
依次访问v的各个未曾访问过的邻接点
分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。重复步骤（3），直至图中所有已被访问的顶点的邻接点都被访问到

对于连通图G4, 遍历路径 $v_1 -> v_2 -> v_3 -> v_4 -> v_5 -> v_6 -> v_7 -> v_7$

#include <stdio.h>
#include <stdlib.h>

#define MAX_VERTICES 100

typedef struct Node {
    int vertex;
    struct Node* next;
} Node;

typedef struct Graph {
    int numVertices;
    Node* adjLists[MAX_VERTICES];
} Graph;

// 链队
typedef struct QNode QNode;
typedef struct QNode* QPtr;

struct QNode
{
    int data;
    struct QNode* next;
};

typedef struct LinkQueue LinkQueue;
struct LinkQueue
{
    QPtr front; // 队头指针
    QPtr rear;  // 队尾指针
};

// InitQueue 链队初始化
// 1、生成新结点，队头和队尾都指向此结点
// 2、头结点的指针域置为空
void InitQueue(LinkQueue *q)
{
    QPtr node = (QPtr)malloc(sizeof(QNode));
    node->next = NULL;
    q->front = node;
    q->rear = node;
}

// EnQueue 元素入队
// 1、为入队元素分配结点空间，用指针p指向
// 2、将新结点数据域置为e
// 3、将新结点插入到队尾
// 4、修改队尾指针为p
void EnQueue(LinkQueue *q, int e)
{
    QPtr p = (QPtr)malloc(sizeof(QNode));
    p->data = e;
    p->next = NULL;
    q->rear->next = p;
    q->rear = p;
}

// DeQueue 元素出队
// 1、判断队列是否为空，若空则返回-1
// 2、临时保存队头元素的空间，以备释放
// 3、修改头结点的指针域，指向下一个结点
// 4、判断出队是否为最后一个元素，若是，则将队尾指针重新赋值，指向头结点
// 5、释放原队头元素的空间
void DeQueue(LinkQueue *q, int *e)
{
    if (q->rear == q->front)
    {
        return;
    }
    QPtr p = q->front->next;
    *e = p->data;
    q->front->next = p->next;
    if (q->rear == p)
    {
        q->rear = q->front;
    }
    free(p);
}

// 创建图
Graph* createGraph(int vertices) {
    Graph* graph = malloc(sizeof(Graph));
    graph->numVertices = vertices;

    for (int i = 0; i < vertices; i++) {
        graph->adjLists[i] = NULL;
    }
    return graph;
}

// 创建节点
Node* createNode(int v) {
    Node* newNode = malloc(sizeof(Node));
    newNode->vertex = v;
    newNode->next = NULL;
    return newNode;
}

// 添加边
void addEdge(Graph* graph, int src, int dest) {
    Node* newNode = createNode(dest);
    newNode->next = graph->adjLists[src];
    graph->adjLists[src] = newNode;

    newNode = createNode(src);
    newNode->next = graph->adjLists[dest];
    graph->adjLists[dest] = newNode;
}

// 查找第一个邻接顶点
int FirstAdjVex(Graph* graph, int vertex) {
    Node* adjList = graph->adjLists[vertex];
    if (adjList != NULL) {
        return adjList->vertex; // 返回第一个邻接顶点
    }
    return -1; // 如果没有邻接顶点，返回-1
}

// 查找下一个邻接顶点
int NextAdjVex(Graph* graph, int vertex, int current) {
    Node* adjList = graph->adjLists[vertex];
    while (adjList != NULL) {
        if (adjList->vertex == current) {
            if (adjList->next != NULL) {
                return adjList->next->vertex; // 返回下一个邻接顶点
            } else {
                return -1; // 如果没有下一个邻接顶点，返回-1
            }
        }
        adjList = adjList->next;
    }
    return -1; // 如果没有找到当前顶点，返回-1
}

// 广度优先搜索
void BFS(Graph* graph, int vertex, int* visited) {
    visited[vertex] = 1; // 标记为已访问
    printf("Visited %d\n", vertex);
    LinkQueue *queue = (LinkQueue*)malloc(sizeof(LinkQueue));
    InitQueue(queue);

    EnQueue(queue, vertex);
    while (queue->rear != queue->front)
    {
        DeQueue(queue, vertex);
        int adjVertex = FirstAdjVex(graph, vertex);
        while (adjVertex != -1) {
            if (!visited[adjVertex]) {
                visited[adjVertex] = 1;
                printf("Visited %d\n", adjVertex);
                EnQueue(queue, adjVertex);
            }
            adjVertex = NextAdjVex(graph, vertex, adjVertex);
        }
    }
}

// 打印图
void printGraph(Graph* graph) {
    for (int v = 0; v < graph->numVertices; v++) {
        Node* temp = graph->adjLists[v];
        printf("Vertex %d: ", v);
        while (temp) {
            printf("%d -> ", temp->vertex);
            temp = temp->next;
        }
        printf("NULL\n");
    }
}

int main() {
    Graph* graph = createGraph(5);

    addEdge(graph, 0, 1);
    addEdge(graph, 0, 4);
    addEdge(graph, 1, 2);
    addEdge(graph, 1, 3);
    addEdge(graph, 1, 4);
    addEdge(graph, 2, 3);
    addEdge(graph, 3, 4);

    printGraph(graph);

    int visited[MAX_VERTICES] = {0}; // 访问标记数组
    printf("Depth First Search starting from vertex 0:\n");
    DFS(graph, 0, visited);

    return 0;
}

图的应用

最小生成树

MST性质: 假设N=(V,E)是一个连通网,U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中 $u \in U, v \in V-U$ ，则必定存在一棵包含边(u, v)的最小生成树

普里姆算法

时间复杂度为O(n2)，与网中的边数无关，因此适用于求稠密网的最小生成树

构造过程

假设N=(V, E)是连通网，TE是N上最小生成树中边的集合

$U={ u_0 } (u_0 \in V), \quad TE = {}$
在所有$u \in U, \quad v \in V-U$的边$(u, v) \in E$ 中找一条权值最小的边 $(u_0, v_0)$ 并入集合TE，同时 $v_0$ 并入U
重复步骤2，直到U=V为止此时TE中必有n-1条边，则T=(V, TE)为N的最小生成树

算法实现

#define MaxInt 32767 // 表示极大值∞
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct
{
    VerTexType vexs[MVNum]; // 顶点表
    ArcType arcs[MVNum][MVNum]; // 邻接矩阵
    int vexnum, arcnum; // 图的当前顶点数和边数
}AMGraph;

// 辅助数组，用来记录从顶点集U到V-U的权值最小的边
struct {
    VerTexType adjvex; // 最小边在U中的顶点位置
    ArcType lowcost; // 最小边的权值
}closedge[MVNum];

// 确定顶点v的在图中的位置
int LocateVex(AMGraph *g, VerTexType v)
{
    for (int i = 0; i < g->vexnum; i++)
    {
        if (g->vexs[i] == v)
        {
            return i;
        }
    }
    return -1;
}

int Min()
{
    int min = 10000;
    int k = 0;
    for (int i = 0; i < MVNum; i++)
    {
        if (closedge[i].lowcost != 0 && closedge[i].lowcost < min) {
            min = closedge[i].lowcost;
            k = i;
        }
    }
    return k;
}

// 无向网G以邻接矩阵形式存储，从顶点u出发构造G的最小生成树T，输入T的各条边
void MiniSpanTree(AMGraph *g, VerTexType u)
{
    int k = LocateVex(g, u);
    // 对V-U的每一个顶点vi, 初始化closedge[i]
    for (int i = 0; i < g->vexnum; i++)
    {
        if (i != k)
        {
            closedge[i].adjvex = u;
            closedge[i].lowcost = g->arcs[k][i];
        }
    }
    // 初始U = {u}
    closedge[k].lowcost = 0;

    // 选择其余n-1个顶点，生成n-1条边(n=g->vexnum)
    for (int i = 1; i < g->vexnum; i++)
    {
        // 求出T的下一个结点: 第k个顶点，closedge[k]中存有当前最小边
        int k = Min();
        // u0为最小边的一个顶点，u0∈U
        VerTexType u0 = closedge[k].adjvex;
        // v0位最小边的另一个顶点，v0∈V-U
        VerTexType v0 = g->vexs[k];
        printf("%c\t%c\n", v0, u0);
        // 第k个顶点并入U集
        closedge[k].lowcost = 0;
        for (int j = 0; j < g->vexnum; j++)
        {
            // 新顶点并入U后重新选择最小边
            if (g->arcs[k][j] < closedge[j].lowcost)
            {
                closedge[j].adjvex = g->vexs[k];
                closedge[j].lowcost = g->arcs[k][j];
            }
        }
    }
}

克鲁斯卡尔算法

时间复杂度为O(elog2e)，与网中的边数有关，与普里姆算法相比，克鲁斯卡尔算法更适合于求稀疏网的最小生成树

构造过程

假设连通网N=(V, E)，将N中的边按权值从小到大的顺序排列

初始状态为只有n个顶点而无边的非连通图T=(V, {})，图中每个顶点自成一个连通分量
在E中选择权值最小的边，若该边依附的顶点落在T中不同的连通分量上(即不形成回路)，则将此边加入到T中，否则舍去此边而选择下一条权值最小的边
重复步骤2，直至T中所有顶点都在同一连通分量上为止

算法实现

结构体Edge：存储边的信息，包括边的两个顶点信息和权值

Vexset[i]：标识各个顶点所属的连通分量。对每个顶点vi∈V，在辅助数组中存在一个相应元素Vexset[i]表示该顶点所在的连通分量。初始时Vexset[i]=i，表示各顶点自成一个连通分量

将数组edges中的元素按权值从小到大排序
依次查看数组edges的边，循环执行以下操作 a. 依次从排好序的数组edges中选出一条边 $(U_1, U_2)$ b. 在Vexset中分别查找 $v_1$ 和 $v_2$ 所在的连通分量 $vs_1$ 和 $vs_2$ ，进行判断
- 如果 $vs_1$ 和 $vs_2$ 不等，表明所选的两个顶点分属不同的连通分量，输出此边，并合并 $vs_1$ 和 $vs_2$ 两个连通分量
- 如果 $vs_1$ 和 $vs_2$ 相等，表明所选的两个顶点属于同一个连通分量，舍去此边而选择下一条权值最小的边

#include <stdlib.h>
#define MaxInt 32767 // 表示极大值∞
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct
{
    VerTexType vexs[MVNum]; // 顶点表
    ArcType arcs[MVNum][MVNum]; // 邻接矩阵
    int vexnum, arcnum; // 图的当前顶点数和边数
}AMGraph;

// 结构体数组Edge：存储边的信息，包括边的两个顶点信息和权值。
typedef struct
{
    VerTexType head; // 边的始点
    VerTexType tail; // 边的终点
    ArcType lowcost; // 边的权值
}Edge;

// 辅助数组
int Vexset[MVNum];

// 确定顶点v的在图中的位置
int LocateVex(AMGraph *g, VerTexType v)
{
    for (int i = 0; i < g->vexnum; i++)
    {
        if (g->vexs[i] == v)
        {
            return i;
        }
    }
    return -1;
}

// 比较函数，用于边的排序
int compare(const void *a, const void *b) {
    Edge *edgeA = (Edge *)a;
    Edge *edgeB = (Edge *)b;
    return edgeA->lowcost - edgeB->lowcost;
}

// 无向网G以邻接矩阵形式存储，从顶点u出发构造G的最小生成树T，输入T的各条边
void MiniSpanTree(AMGraph *g, VerTexType u)
{
    // 从邻接矩阵中提取边
    Edge edges[g->vexnum];
    int edgeCount = 0;
    for (int i = 0; i < g->vexnum; i++) {
        for (int j = i + 1; j < g->vexnum; j++) {
            if (g->arcs[i][j] != MaxInt) {
                edges[edgeCount].head = i;
                edges[edgeCount].tail = j;
                edges[edgeCount].lowcost = g->arcs[i][j];
                edgeCount++;
            }
        }
    }
    qsort(edges, edgeCount, sizeof(edges[0]), compare);

    // 表示各顶点自成一个连通分量
    for (int i = 0; i < g->vexnum; i++)
    {
        Vexset[i] = i;
    }

    for (int i = 0; i < g->arcnum; i++)
    {
        int v1 = LocateVex(g, edges[i].head);
        int v2 = LocateVex(g, edges[i].tail);
        int vs1 = Vexset[v1]; // 获取边Edge[i]的始点所在的连通分量
        int vs2 = Vexset[v2]; // 获取边Edge[i]的终点所在的连通分量
        // 边的两个顶点分属不同的连通分量
        if (vs1 != vs2)
        {
            printf("%d\t%d\n", edges[i].head, edges[i].tail);
            // 合并vs1和vs2两个分量，即两个集合统一编号
            for (int j = 0; j < g->vexnum; j++)
            {
                if (Vexset[j] == vs2)
                {
                    Vexset[j] == vs1;
                }
            }
        }
    }
}

最短路径

从某个源点到其余各顶点的最短路径

给定带权有向图G和源点 $v_0$ ，求从 $v_0$ 到G中其余各顶点的最短路径 Dijkstra算法：按路径长度递减的次序产生最短路径

求解过程

对于网N=(V,E)，将N中顶点分成两组: 第一组S：已求出的最短路径的终点集合(初始时只包含源点 $v_0$ ) 第二组V-S：尚未求出的最短路径的集合(初始时为V-{ $v_0$ })

算法将按各顶点与 $v_0$ 间最短路径长度递增的次序，逐个将集合V-S中的顶点加入到集合S中去。在这个过程中，总保持 $v_0$ 到集合S中各顶点的路径长度始终不大于到集合V-S中各顶点的路径长度

算法实现

假设用带权的邻接矩阵arcs来表示带权有向网G，G.arcs[i][j]表示弧 $<v_i, v_j>$ 上的权值。若 $<v_i, v_j>$ 不存在，则置G.arcs[i][j]为 $\infty$ ，源点为 $v_0$

算法的实现引入以下辅助数组的数据结构:

一维数组S[i]：记录从源点 $v_0$ 到终点 $v_i$ 是否已被确定为最短路径长度，true表示确定, false表示尚未确定
一维数组Path[i]：记录从源点 $v_0$ 到终点 $v_i$ 的当前最短路径上 $v_i$ 的直接前驱顶点序号。其初值为：如果从 $v_0$ 到$v_i$ 有弧，则Path[i]为 $v_0$ ，否则为-1
一维数组D[i]：记录从源点 $v_0$ 到终点 $v_i$ 的当前最短路径长度。其初值为：其初值为：如果从 $v_0$ 到 $v_i$ 有弧，则D[i]为弧上的权值，否则为 $\infty$

步骤如下

初始化：
- 将源点 $v_0$ 加到S中，即S[ $v_0$ ]=true;
- 将 $v_0$ 到各个终点的最短路径长度初始为权值，即D[i]=G.arcs[ $v_0$ ][ $v_i$ ], ( $v_i \in V-S$ )
- 如果 $v_0$ 和顶点 $v_i$ 之间有弧，则将 $v_i$ 的前驱值为 $v_0$ ，即Path[i]= $v_0$ ，否则Path[i]=-1
循环n-1次，执行以下操作: a. 选择下一条最短路径的终点 $v_k$ ，使得： $D[k] = Min{D[i] \quad | \quad v_i \in V-S}$ b. 将$v_k$加到S中，即S[ $v_k$ ]=true c. 根据条件更新从 $v_0$ 出发到集合V-S上任一顶点的最短路径的长度。若条件D[k]+G.arcs[k][i] < D[i]成立，则更新D[i]=D[k]+G.arcs[k][i]，同时更改 $v_i$ 的前驱为 $v_k$ ，Paht[i]=k

#define MaxInt 32767 // 表示极大值∞
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct
{
    VerTexType vexs[MVNum]; // 顶点表
    ArcType arcs[MVNum][MVNum]; // 邻接矩阵
    int vexnum, arcnum; // 图的当前顶点数和边数
}AMGraph;

// Dijkstra算法求有向网G的v0顶点到其余顶点的最短距离
void ShortestPath(AMGraph *g, int v0)
{
    int s[g->vexnum]; // 0表示false, 1表示true
    int path[g->vexnum];
    int d[g->vexnum];
    int n = g->vexnum;
    for (int v = 0; v < n; v++)
    {
        s[v] = 0; // s初始为空集
        d[v] = g->arcs[v0][v]; // 将v0到各个顶点的最短路径长度初始为弧上的权值
        // 如果v0和v之间有弧，则将v的前驱置为v0
        if (d[v] < MaxInt) {
            path[v] = v0;
        } else
        {
            // 如果v0和v之间无弧，则将v的前驱置为-1
            path[v] = -1;
        }
    }

    s[v0] = 1; // 将v0加入s
    d[v0] = 0; // 源点到源点的距离为零

    for (int i = 1; i < n; i++)
    {
        int v = 0;
        int min = MaxInt;
        for (int w = 0; w < n; w++)
        {
            if (s[w] == 0 && d[w] < min)
            {
                v = w;
                min = d[w];
            }
        }
        s[v] = 1; // 将v加入s
        for (int w = 0; w < n; w++)
        {
            if (s[w] == 0 && d[v] + g->arcs[v][w] < d[w])
            {
                d[w] = d[v] + g->arcs[v][w];
                path[w] = v; // 更新w的前驱为v
            }
        }
    }
}

每一对顶点之间的最短路径

Floyd算法：使用带权的邻接矩阵arcs来表示有向网G，求从顶点 $v_i$ 到 $v_j$ 的最短路径

算法实现

辅助数据结构

二维数组Path[i][j]：最短路径上顶点 $v_j$ 的前一顶点的序号
二维数组D[i][j]：记录顶点 $v_i$ 和顶点 $v_j$ 之间的最短路径长度

步骤如下

将 $v_i$ 到 $v_j$ 的最短路径长度初始化，即D[i][j]=G.arcs[i][j]，然后进行n次比较和更新

在 $v_i$ 和 $v_j$ 间加入顶点 $v_0$ ，比较 $(v_i, v_j)$ 和 $(v_i, v_0, v_j)$ 的路径长度，取其中较短者作为 $v_i$到 $v_j$ 的中间顶点序号不大于0的最短路径
在 $v_i$ 和 $v_j$ 间加入 $v_1$ , 得到 $(v_j, \cdots, v_1)$ 和 $(v_1, \cdots, v_j)$ ，其中 $(v_j, \cdots, v_1)$ 是 $v_j$ 到 $v_1$ 的且中间顶点的序号不大于0的最短路径， $(v_1, \cdots, v_j)$ 是 $v_1$ 到 $v_j$ 的且中间顶点序号不大于0的最短路径，这两条路径已在上一步中求出。比较 $(v_i, \cdots, v_1, \cdots, v_j)$ 与上一步求出的 $v_i$ 到 $v_j$ 的中间顶点序号不大于0的最短路径，取其中较短者作为 $v_i$ 到 $v_j$ 的中间顶点序号不大于1的最短路径
依此类推，在 $v_i$ 和 $v_j$ 间加入顶点 $v_k$ ，若 $(v_i, \cdots, v_k)$ 和 $(v_k, \cdots, v_j)$ 分别是 $v_i$ 到 $v_k$ 和 $v_k$ 到 $v_j$ 的中间顶点序号不大于k-1的最短路径，则将 $(v_i, \cdots, v_k, \cdots, v_j)$ 和已经得到的从 $v_i$ 到 $v_j$ 且中间顶点序号不大于k-1的最短路径相比较，其长度较短者便是从 $v_i$ 到 $v_j$ 的中间顶点序号不大于k的最短路径。这样，经过n次比较后，最后求得的必是从 $v_i$ 到 $v_j$ 的最短路径

#define MaxInt 32767 // 表示极大值∞
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct
{
    VerTexType vexs[MVNum]; // 顶点表
    ArcType arcs[MVNum][MVNum]; // 邻接矩阵
    int vexnum, arcnum; // 图的当前顶点数和边数
}AMGraph;

// Floyd算法求有向网G中各对顶点i和j之间的最短路径
void ShortestPath(AMGraph *g)
{
    int path[MVNum][MVNum];
    int d[MVNum][MVNum];
    for (int i = 0; i < g->vexnum; i++)
    {
        for (int j = 0; j < g->vexnum; j++)
        {
            d[i][j] = g->arcs[i][j];
            if (d[i][j] < MaxInt)
            {
                // 如果i和j之间有弧，则将j的前驱置为i
                path[i][j] = i;
            } else
            {
                // 如果i和j之间无弧，则将j的前驱置为-1
                path[i][j] = -1;
            }
        }
        for (int k = 0; k < g->vexnum; g++)
        {
            for (int i = 0; i < g->vexnum; i++)
            {
                for (int j = 0; j < g->vexnum; j++)
                {
                    // 从i经k到j的一条路径更短
                    if (d[i][k] + d[k][j] < d[i][j])
                    {
                        d[i][j] = d[i][k] + d[k][j];
                        path[i][j] = path[k][j]; // 更改j的前驱为k
                    }
                }
            }
        }
    }
}

拓扑排序

拓扑排序过程

在有向图中选一个无前驱的顶点且输出它
从图中删除该顶点和所有以它为尾的弧
重复1和2，直至不存在无前驱的顶点
若此时输出的顶点数小于有向图中的顶点数，则说明有向图中有环，否则输出的顶点序列即为一个拓扑序列

拓扑排序实现

辅助数据结构

一维数组indegree[i]：存放各顶点入度，没有前驱的顶点就是入度为零的顶点。删除顶点及以它为尾的弧的操作，可不必真正为图的存储结构进行改变，可用弧头顶点的入度减1的办法来实现
栈s：暂存所有入度为零的顶点，这样可以避免重复扫描数组indegree检测入度为零的顶点，提高算法效率
一维数组topo[i]：记录拓扑序列的顶点序号

算法步骤

求出各顶点的入度存入数组indegree[i]中，并将入度为零的顶点入栈
只要栈不空，则重复以下操作: a. 将栈顶顶点 $v_i$ 出栈并保存在拓扑数组topo中 b. 对顶点 $v_i$ 的每个邻接点 $v_k$ 的入度减1，如果 $v_k$ 的入度变为0，则将 $v_k$ 入栈
如果输出顶点个数少于AOV-网的顶点个数，则网中存在环，无法进行拓扑排序，否则拓扑排序成功

#include<stdio.h>
#include<stdlib.h>
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型
typedef int ArcType; // 假设边的权值类型为整型

typedef struct ArcNode {
    int adjvex; // 该边所指向的顶点的位置
    struct ArcNode *nextarc; // 指向下一条边的指针
}ArcNode;

typedef struct VNode {
    VerTexType data;
    ArcNode *firstarc; // 指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum];

typedef struct ALGraph {
    AdjList vertices;
    int vexnum, arcnum; // 图的当前顶点数和边数
}ALGraph;

typedef struct StackNode
{
    int data;
    struct StackNode* next;
}StackNode,*LinkStack;

// InitStack 初始化链栈
int InitStack(LinkStack s) {
    s = NULL;
    return 0;
}

// Push 入栈
// 1. 为入栈元素分配空间,用指针p指向
// 2. 将新节点数据域置为e
// 3. 将新节点插入栈顶
// 4. 修改栈顶指针为p
LinkStack Push(LinkStack s, int e) {
    LinkStack p = (LinkStack)malloc(sizeof(StackNode));
    p->data = e;
    p->next = s;
    s = p;
    return s;
}

// Pop 出栈
// 1. 判断栈是否为空,若空则返回-1
// 2. 将栈顶元素赋给e
// 3. 临时保存栈顶元素的地址,以备释放
// 4. 修改栈顶指针,指向新的栈顶元素
// 5. 释放原栈顶元素的地址
LinkStack Pop(LinkStack s, int *e) {
    if (s == NULL) {
        return s;
    }
    *e = s->data;
    LinkStack p = s;
    s = s->next;
    free(p);
    return s;
}

// 求顶点入度
void FindInDegree(ALGraph *g, int indegree[])
{
    for (int i = 0; i < g->vexnum; i++)
    {
        indegree[i] = 0;
    }
    for (int i = 0; i < g->vexnum; i++)
    {
        ArcNode *p = g->vertices[i].firstarc;
        while (p)
        {
            indegree[p->adjvex]++;
            p = p->nextarc;
        }
    }
}

// 有向图G采用邻接表存储结构
// 若G无回路，则生成G的一个拓扑序列topo[]并返回1，否则返回0
int TopologicalSort(ALGraph *g, int topo[])
{
    int indegree[MVNum];
    FindInDegree(g, indegree);

    LinkStack s;
    InitStack(s);
    for (int i = 0; i < g->vexnum; i++)
    {
        if (indegree[i] == 0)
        {
            Push(s, i);
        }
    }

    int m = 0;
    while (s != NULL)
    {
        int i;
        // 栈顶顶点vi出栈
        Pop(s, &i);
        // 将vi保存在拓扑序列数组topo中,并对输出顶点计数
        topo[m++] = i;
        // p指向vi的第一个邻接点
        ArcNode *p = g->vertices[i].firstarc;
        while (p != NULL)
        {
            // vk为vi的邻接点
            int k = p->adjvex;
            // vi的每个邻接点的入度减1
            --indegree[k];
            // 若vk顶点入度为0，则入栈
            if (indegree[k] == 0)
            {
                Push(s, k);
            }
            // p指向顶点vi的下一个邻接点
            p = p->nextarc;
        }
    }
    if (m < g->vexnum)
    {
        return 0;
    }
    return 1;
}

关键路径

求解过程

对图中顶点进行排序，在排序过程中按拓扑序列求出每个事件的最早发生时间ve(i)
按逆拓扑序列求出每个事件的最迟发生时间vl(i)
求出每个活动 $a_i$ 的最早开始时间e(i)
求出每个活动 $a_i$ 的最晚开始时间l(i)
找出e(i)=l(i)的活动 $a_i$ ，即位关键活动。由关键活动形成的由源点到汇点的每一条路径就是关键路径，关键路径有可能不止一条

算法实现

由于每个事件的最早发生时间ve(i)和最迟发生时间vl(i)要在拓扑序列的基础上进行计算，所以关键路径算法的实现要基于拓扑排序算法，采用邻接表做有向图的存储结构

辅助数据结构

一维数组ve[i]：事件 $v_i$ 的最早发生时间
一维数组vl[i]：事件 $v_i$ 的最迟发生时间
一维数组topo[i]：记录拓扑序列的顶点序号

算法步骤

调用拓扑排序算法，使拓扑序列保存在数组topo中
将每个事件的最早发生时间ve[i]初始化为零
根据topo中的值，按从前向后的拓扑次序，依次求每个事件的最早发生时间，循环几次，执行以下操作： a. 取得拓扑序列中的顶点序号k，k=topo[i] b. 用指针p依次指向k的每个邻接顶点，取得每个邻接顶点的序号j=p->adjvex，依次更新顶点j的最早发生时间ve[j] $if (ve[j] < ve[k]+p->weight) ve[j] = ve[k] + p->weight;$
将每个事件的最迟发生时间vl[i]初始化为汇点的最早发生时间, vl[i]=ve[n-1]
根据topo中的值，按从后向前的逆拓扑次序，依次求每个时间的最迟发生时间，循环n次，执行以下操作： a. 取得拓扑序列中的顶点序号k，k=topo[i] b. 用指针p依次指向k的每个邻接顶点，取得每个邻接顶点的序号j=p->adjvex，依次根据k的邻接点，更新k的最迟发生时间vl[k] $if (vl[k] > vl[j] - p->weight) vl[k] = vl[j] - p->weight$
判断某一活动是否为关键活动，循环n次，执行以下操作：对于每个顶点i，用指针p依次指向i的每个邻接点，取得每个邻接顶点的序号j=p->adjvex，分别计算活动< $v_i$ , $v_j$ >的最早和最迟发生时间e和l，e=ve[i];l=vl[j]-p->weight;。如果e和l相等，则活动< $v_i$ , $v_j$ >为关键活动，输出弧 $v_j$

#include<stdio.h>
#include<stdlib.h>
#define MVNum 100 // 最大顶点数

typedef char VerTexType; // 假设顶点的数据类型是字符型

typedef struct ArcNode {
    int adjvex; // 该边所指向的顶点的位置
    int weight; // 权值
    struct ArcNode *nextarc; // 指向下一条边的指针
}ArcNode;

typedef struct VNode {
    VerTexType data;
    ArcNode *firstarc; // 指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum];

typedef struct ALGraph {
    AdjList vertices;
    int vexnum, arcnum; // 图的当前顶点数和边数
}ALGraph;

typedef struct StackNode
{
    int data;
    struct StackNode* next;
}StackNode,*LinkStack;

// InitStack 初始化链栈
int InitStack(LinkStack s) {
    s = NULL;
    return 0;
}

// Push 入栈
// 1. 为入栈元素分配空间,用指针p指向
// 2. 将新节点数据域置为e
// 3. 将新节点插入栈顶
// 4. 修改栈顶指针为p
LinkStack Push(LinkStack s, int e) {
    LinkStack p = (LinkStack)malloc(sizeof(StackNode));
    p->data = e;
    p->next = s;
    s = p;
    return s;
}

// Pop 出栈
// 1. 判断栈是否为空,若空则返回-1
// 2. 将栈顶元素赋给e
// 3. 临时保存栈顶元素的地址,以备释放
// 4. 修改栈顶指针,指向新的栈顶元素
// 5. 释放原栈顶元素的地址
LinkStack Pop(LinkStack s, int *e) {
    if (s == NULL) {
        return s;
    }
    *e = s->data;
    LinkStack p = s;
    s = s->next;
    free(p);
    return s;
}

// 求顶点入度
void FindInDegree(ALGraph *g, int indegree[])
{
    for (int i = 0; i < g->vexnum; i++)
    {
        indegree[i] = 0;
    }
    for (int i = 0; i < g->vexnum; i++)
    {
        ArcNode *p = g->vertices[i].firstarc;
        while (p)
        {
            indegree[p->adjvex]++;
            p = p->nextarc;
        }
    }
}

// 有向图G采用邻接表存储结构
// 若G无回路，则生成G的一个拓扑序列topo[]并返回1，否则返回0
int TopologicalSort(ALGraph *g, int topo[])
{
    int indegree[MVNum];
    FindInDegree(g, indegree);

    LinkStack s;
    InitStack(s);
    for (int i = 0; i < g->vexnum; i++)
    {
        if (indegree[i] == 0)
        {
            Push(s, i);
        }
    }

    int m = 0;
    while (s != NULL)
    {
        int i;
        // 栈顶顶点vi出栈
        Pop(s, &i);
        // 将vi保存在拓扑序列数组topo中,并对输出顶点计数
        topo[m++] = i;
        // p指向vi的第一个邻接点
        ArcNode *p = g->vertices[i].firstarc;
        while (p != NULL)
        {
            // vk为vi的邻接点
            int k = p->adjvex;
            // vi的每个邻接点的入度减1
            --indegree[k];
            // 若vk顶点入度为0，则入栈
            if (indegree[k] == 0)
            {
                Push(s, k);
            }
            // p指向顶点vi的下一个邻接点
            p = p->nextarc;
        }
    }
    if (m < g->vexnum)
    {
        return 0;
    }
    return 1;
}

// g为邻接表存储的有向图，输出g的各项关键活动
int CriticalPath(ALGraph *g)
{
    int topo[g->vexnum];
    int ve[g->vexnum];
    int vl[g->vexnum];
    if (TopologicalSort(g, topo) == 0)
    {
        return 0;
    }

    // 每个事件的最早发生时间初始化为零
    for (int i = 0; i < g->vexnum; i++)
    {
        ve[i] = 0;
    }

    // 按拓扑次序求每个事件的最早发生时间
    for (int i = 0; i < g->vexnum; i++)
    {
        int k = topo[i];
        // 取得拓扑序列中的顶点序号k
        ArcNode *p = g->vertices[k].firstarc;
        // 依次更新k的所有邻接点的最早发生时间
        while (p != NULL)
        {
            int j = p->adjvex;
            if (ve[j] < ve[k] + p->weight) {
                ve[j] = ve[k] + p->weight;
            }
            p = p->nextarc;
        }
    }

    // 每个事件的最迟发生时间初始为ve[n-1]
    for (int i = 0; i < g->vexnum; i++)
    {
        vl[i] = ve[g->vexnum-1];
    }
    // 按逆拓扑排序求每个事件的最迟发生时间
    for (int i = g->vexnum-1; i >= 0; i--)
    {
        int k = topo[i];
        ArcNode *p = g->vertices[k].firstarc;
        while (p != NULL)
        {
            int j = p->adjvex;
            if (vl[k] > vl[j] - p->weight)
            {
                vl[k] = vl[j] - p->weight;
            }
            p = p->nextarc;
        }
    }

    // 判断每一活动是否为关键活动
    for (int i = 0; i < g->vexnum; i++)
    {
        ArcNode *p = g->vertices[i].firstarc;
        while (p != NULL)
        {
            int j = p->adjvex;
            int e = ve[i];
            int l = vl[j] - p->weight;
            if (e == l)
            {
                printf("关键活动: %c -> %c\n", g->vertices[i].data, g->vertices[j].data);
            }
            p = p->nextarc;
        }
    }
}