图
子图 : 假设有两个图G=(V,E),G'=(V',E'),
若V'是V的子集且E'是E的子集,则称G'是G的子集
无向完全图和有向完全图 :
对于无向图,若具有n(n-1)/2条边,则称为无向完全图。对于有向图,若具有n(n-1)条弧,则称为有向完全图
稀疏图和稠密图 : 有很少条边或弧(如\(e<nlog_2n\) )的图称为稀疏图,反之称为稠密图
权和网 :在实际应用中,每条边可以标上具有某种含义的数值,该数值称为该边上的权。这些权可以表示从一个顶点到另一个顶点的距离,这种带权的图通常称为网
邻接点 : 对于无向图G,如果图的边\((v,v') \in
E\) ,则称顶点v和v'互为邻接点,即v和v'相邻接。边(v,v')依附于顶点v和v',
或者说边(v,v')与顶点v和v'相关联
度、入度和出度 :
顶点v的度是指和v相关联的边的数目。对于有向图,顶点v的度分为入度和出度。入度 是以顶点v为头的弧的数目,
出度 是以顶点v为尾的弧的数目
路径和路径长度 :
在无向图中,从顶点v到顶点v'的路径是一个顶点序列(\(v=v_{i,0},v_{i,1},\cdots,v_{i,m}=v'\) ),其中(\(v_{i,j-1},v_{i,j} \in E, 1 \leq j \leq
m\) )。在有向图中,路径也是有向的,顶点序列应满足\(<v_{i,j-1},v_{i,j}> \in E, 1 \leq j \leq
m\) 。路径长度 是一条路径上经过的边或弧的数目
回路或环 :
第一个顶点和最后一个顶底相同的路径称为回路或环
简单路径、简单回路或简单环 :
序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外,其余顶点不重复出现的回路,称为简单回路或简单环
连通、连通图和连通分量 :
在无向图G中,如果从顶点v到顶点v'有路径,则称v和v'是连通的。如果对于图中任意两个顶点\(v_i, v_j \in V, v_i\) 和\(v_j\) 都是连通的,则称G为连通图。所谓连通分量,指的是无向图中极大连通子图
强连通图和强连通分量 :
在有向图G中,如果对于每一对\(v_i,v_j \in V,
v_i \ne v_j\) , 从\(v_i\) 到\(v_j\) 和从\(v_j\) 到\(v_i\) 都存在路径,则称G是强连通图。有向图中的极大连通子图称为有向图的强连通分量
连通图的生成树 :
一个极小连通子图,它含有图中全部顶点,但只有足以构成一棵树的n-1条边,这样的连通子图称为连通图的生成树
有向树和生成森林 :
有一个顶点的入度为0,其余顶点的入度均为1的有向图称为有向树,一个有向图的生成森林是有若干棵有向树组成
图的存储结构
邻接矩阵
优点
便于判断两个顶点之间是否有边,即根据A[i][j]=0或1来判断
便于计算各顶点的度。对于无向图,邻接矩阵第i行元素之和即为顶底i的度;对于有向图,第i行元素的和就是顶点i的出度,第i列元素的和为顶点i的入度
缺点
不便于增加和删除顶点
不便于统计边的数目,需要扫描邻接矩阵所有元素才能统计完毕。时间复杂度为\(O(n^2)\)
空间复杂度高,复杂度为\(O(n^2)\)
用二维数组来表示元素之间的关系
邻接矩阵 是表示顶点之间相邻关系的矩阵。设G(V,E)是具有n个顶点的图,则G的邻接矩阵是具有如下性质的n阶方阵
\[
A[i][j] = \begin{cases}
1 \qquad <v_i, v_j> \text{或} (v_i, v_j) \in E
\\
0 \qquad \text{反之}
\end{cases}
\]
示例:
\[
G_{1,arcs} = \begin{bmatrix}
0 & 1 & 1 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
1 & 0 & 0 & 0
\end{bmatrix}
\]
G是网
\[
A[i][j] = \begin{cases}
w_{i,j} \qquad \text{若}<v_i, v_j> \text{或} (v_i, v_j) \in E,
\text{表示边上的权值} \\
\infty
\end{cases}
\]
示例:
\[
\begin{bmatrix}
\infty & 5 & \infty & 7 & \infty & \infty \\
\infty & \infty & 4 & \infty & \infty & \infty \\
8 & \infty & \infty & \infty & \infty & 9 \\
\infty & \infty & 5 & \infty & \infty & 6 \\
\infty & \infty & \infty & 5 & \infty & \infty \\
3 & \infty & \infty & \infty & 1 & \infty \\
\end{bmatrix}
\]
创建无向网 时间复杂度\(O(n^2)\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 #define MaxInt 32767 #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct { VerTexType vexs[MVNum]; ArcType arcs[MVNum][MVNum]; int vexnum, arcnum; }AMGraph; int LocateVex (AMGraph *g, VerTexType v) { for (int i = 0 ; i < g->vexnum; i++) { if (g->vexs[i] == v) { return i; } } return -1 ; } int CreateUDN (AMGraph *g) { scanf ("%d%d" , &g->vexnum, &g->arcnum); for (int i = 0 ; i < g->vexnum; ++i) { scanf ("%c" , &g->vexs[i]); } for (int i = 0 ; i < g->vexnum; i++) { for (int j = 0 ; j < g->vexnum; j++) { g->arcs[i][j] = MaxInt; } } VerTexType v1, v2; ArcType w; for (int k = 0 ; k < g->arcnum; k++) { scanf ("%c%c%d" , &v1,&v2,&w); int i = LocateVex(g, v1); int j = LocateVex(g, v2); if (i == -1 || j == -1 ) { return -1 ; } g->arcs[i][j] = w; } return 0 ; }
创建无向图
针对上述代码,做如下改动即可:
初始化邻接矩阵时,将边的权值初始化为0
构造邻接矩阵时,将权值w改为常量1即可
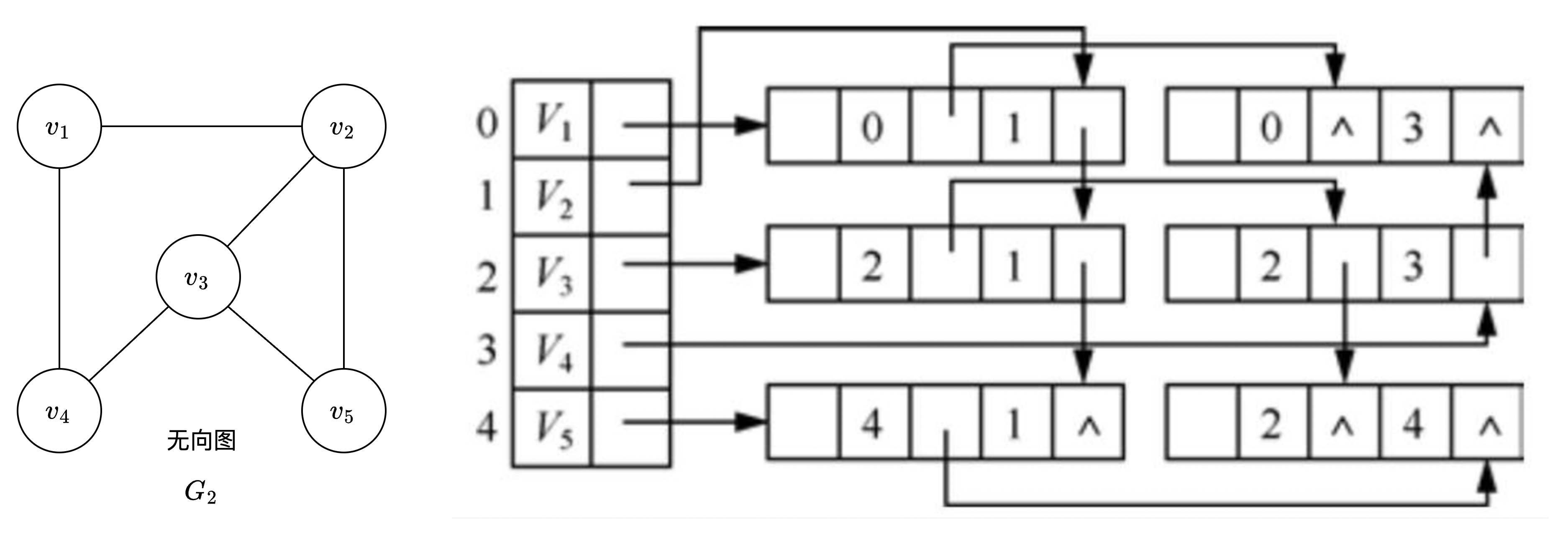
邻接表
邻接表是图的一种链式存储结构。在邻接表中,对图中每个顶点\(v_i\) 建立一个单链表,把与\(v_i\) 相邻接的顶点放在这个链表中。邻接表中每个单链表的第一个结点存放有关顶点的信息,把这一结点看成链表的表头,其余结点存放有关边的信息,这样邻接表便由两部分组成:表头结点表和边表
表头结点表 :
由所有表头结点以顺序结构的形式存储,以便可以随机访问任一顶点的边链表。表头结点包括数据域 和链域 (数据域用于存储顶点\(v_i\) 的名称和其他有关信息;链域用于指向链表中第一个结点即与顶点\(v_i\) 邻接的第一个邻接点)边表 :由表示图中顶点间关系的2n个边链表组成。边链表中边结点包括邻接点域(adjvex)、数据域(info)和邻域(nextarc)三部分
邻接点域指示与顶点\(v_i\) 相邻的点在图中的位置
数据域存储和边相关的信息,如权值等
链域指示与顶点\(v_i\) 邻接的下一条边的结点
\(v_i\) 的度恰为第i个链表中的结点数
* 在有向图中,第i个链表的结点数只是顶点\(v_i\) 的出度;为求入度,必须遍历整个邻接表 *
在所有链表中,其邻接点域的值为i的结点个数是顶点i的入度
逆邻接表 对每个顶点\(v_i\) 建立一个链接所有进入\(v_i\) 的边的表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 #include <stdio.h> #include <stdlib.h> #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct OtherInfo {}OtherInfo; typedef struct ArcNode { int adjvex; struct ArcNode *nextarc ; OtherInfo into; }ArcNode; typedef struct VNode { VerTexType data; ArcNode *firstarc; }VNode, AdjList[MVNum]; typedef struct ALGraph { AdjList vertices; int vexnum, arcnum; }ALGraph; int LocateVex (ALGraph *g, VerTexType v) { for (int i = 0 ; i < g->vexnum; i++) { if (g->vertices[i].data == v) { return i; } } return -1 ; } int CreateUDG (ALGraph *g) { scanf ("%d%d" , &g->vexnum, &g->arcnum); for (int i = 0 ; i < g->vexnum; i++) { scanf ("%c" , &g->vertices[i].data); g->vertices[i].firstarc = NULL ; } for (int k = 0 ; k < g->arcnum; k++) { VerTexType v1, v2; scanf ("%c%c" , &v1, &v2); int i = LocateVex(g, v1); int j = LocateVex(g, v2); if (i == -1 || j == -1 ) { return -1 ; } ArcNode *p1 = (ArcNode*)malloc (sizeof (ArcNode)); p1->adjvex = j; p1->nextarc = g->vertices[i].firstarc; g->vertices[i].firstarc = p1; ArcNode *p2 = (ArcNode*)malloc (sizeof (ArcNode)); p2->adjvex = i; p2->nextarc = g->vertices[j].firstarc; g->vertices[j].firstarc = p2; } return 0 ; }
建立有向图的邻接表与此类似,只是更加简单,每读入一个顶点对序号<i,
j>,仅需生成一个邻接点序号为j的边表结点,并将其插入到\(v_i\) 的边链表头部即可。若要创建网的邻接表,可以将边的权值存储在info域中
优缺点
优点
便于增加和删除顶点
便于统计边的数目,按照顶点表顺序扫描所有边表可得到边的数目,其时间复杂度为O(n+e)
空间效率高。对于一个具有n个顶点e条边的图G,若G是无向图,则其在邻接表表示中有n2eneO(n+e)
缺点
不便于判断顶点之间是否有边,要判定\(v_i\) 和\(v_j\) 之间是否有边,就需要扫描第i个边表,时间复杂度O(n)
不便于计算有向图各个顶点的度。对于无向图,在邻接表表示中顶点\(v_i\) 的度是第i个边表中的结点个数。在有向图的邻接表中,第i个边表上的结点个数是顶点\(v_i\) 的出度,但求\(v_i\) 的入度比较困难,需要遍历各顶点的边表;若有向图采用逆邻接表表示,则与之相反,第i个边表上的结点个数是顶点\(v_i\) 的入度
邻接矩阵和邻接表的比较
比较项目 存储结构
邻接矩阵
邻接表
无向图
有向图
无向图
有向图
空间
邻接矩阵对称,可压缩至n(n-1)/2个单元
邻接矩阵不对称,存储n2 个单元
存储n+2e个单元
存储n+e个单元
时间
求某个顶点vi 的度
扫描邻接矩阵中序号i对应的一行。O(1)
求出度: 扫描矩阵的一行。O(n)
求入度: 扫描矩阵的一列。O(n)
扫描vi 的边表。最坏情况O(n)
求出度: 扫描vi 的边表。最坏情况O(n)
求入度: 按顶点表顺序扫描所有边表。O(n+e)
求边的数目
扫描邻接矩阵。O(n2 )
按顶点表顺序扫描所有边表。O(n+2e)
按顶点表顺序扫描所有边表。O(n+e)
判定边(vi , vj )是否存在
直接检查邻接矩阵A[i][j]元素的值。O(1)
扫描vi 的边表。最坏情况O(n)
使用情况
稠密图
稀疏图
十字链表
十字链表是有向图
弧结点中
尾域(tailvex) : 表示弧尾在图中的结点头域(headvex) : 表示弧头在图中的结点链域(hlink) : 表示指向弧头相同的下一条弧链域(tlink) : 表示指向弧尾相同的下一条弧info域 : 指向该弧的相关信息
弧头相同的弧在同一链表上;弧尾相同的弧也在同一链表上。它们的头结点即为顶点结点。
顶点结点中
data域存储和顶点相关的信息,如顶点的名称等firstin指向以该顶点为弧头的第一个弧结点firstout指向以该顶点为弧尾的第一个弧结点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <stdio.h> #include <stdlib.h> #define MAX_VERTEX_NUM 20 typedef char VertexType;typedef struct InfoType {}InfoType; typedef struct ArcBox { int tailvex, headvex; struct ArcBox *hlink , *tlink ; InfoType *info; }ArcBox; typedef struct VexNode { VertexType data; ArcBox *firstin, *firstout; }VexNode; typedef struct OLGraph { VexNode xlist[MAX_VERTEX_NUM]; int vexnum, arcnum; }OLGraph; int Locate (OLGraph *g, VertexType x) { for (int i = 0 ; i < g->vexnum; i++) { if (g->xlist[i].data == x) { return i; } } return -1 ; } int createGraph (OLGraph *g) { printf ("请输入图的顶点数和狐数\n" ); scanf ("%d%d" , &g->arcnum, &g->vexnum); printf ("请依次输入每个顶点\n" ); for (int i = 0 ; i < g->vexnum; i++) { scanf ("%c" , &g->xlist[i].data); g->xlist[i].firstin = NULL ; g->xlist[i].firstout = NULL ; } printf ("请依次输入每条狐的起点和终点\n" ); for (int k = 0 ; k < g->arcnum; k++) { VertexType x, y; scanf ("%c%c" , &x, &y); int i = Locate(g, x); int j = Locate(g, y); if (i == -1 || j == -1 ) { return -1 ; } ArcBox *node = (ArcBox*)malloc (sizeof (ArcBox)); node->headvex = i; node->tailvex = j; node->hlink = g->xlist[i].firstin; g->xlist[i].firstin = node; node->tlink = g->xlist[i].firstout; g->xlist[i].firstout = node; } return 0 ; }
邻接多重表
邻接多重表是无向图 \((v_i,v_j)\) 有两个结点,分别在第i和第j个链表中,这给某些图得操作带来不便,而采用邻接多重表得无向图更为适宜解决这一类问题
在邻接多重表中,每一条边用一个结点表示,由如下所示得6个域组成:
mark标志域:标记该条边是否被搜索过ivex和jvex:该边依附得两个顶点在图中得位置ilink:指向下一条依附于顶点ivex的边jlink:指向下一条依附于顶点jvex的边info:指向和边相关的各种信息的指针域
每一个顶点也用一个结点表示,由如下所示2个域组成:
data:data域存储和顶点相关的信息firstedge:firstedge域指示第一条依附于该顶点的边
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 #include <stdio.h> #include <stdlib.h> #define MAX_VERTEX_NUM 20 typedef enum {typedef char VertexType;typedef struct InfoType {}InfoType; typedef struct EBox { VisitIf mark; int ivex, jvex; struct EBox *ilink , *jlink ; InfoType *info; }EBox; typedef struct VexBox { VertexType data; EBox *firstedge; }VexBox; typedef struct AMLGraph { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; }AMLGraph; int Locate (AMLGraph *g, VertexType x) { for (int i = 0 ; i < g->vexnum; i++) { if (g->adjmulist[i].data == x) { return i; } } return -1 ; } int createUDG (AMLGraph *g) { printf ("输入顶点数,边数\n" ); scanf ("%d,%d,%d" , &g->vexnum, &g->edgenum); printf ("请输入顶点数\n" ); for (int i = 0 ; i < g->vexnum; i++) { scanf ("%c" , &g->adjmulist[i].data); g->adjmulist[i].firstedge = NULL ; } printf ("请依次输入每条狐的起点和终点\n" ); for (int k = 0 ; k < g->edgenum; k++) { VertexType x, y; scanf ("%c%c" , &x, &y); int i = Locate(g, x); int j = Locate(g, y); if (i == -1 || j == -1 ) { return -1 ; } EBox *box = (EBox *)malloc (sizeof (EBox)); box->ivex = i; box->jvex = j; box->mark = unvisited; box->ilink = g->adjmulist[i].firstedge; box->jlink = g->adjmulist[j].firstedge; g->adjmulist[j].firstedge = box; g->adjmulist[i].firstedge = box; } return 0 ; }
图的遍历
深度优先搜索
类似于树的先序遍历
从图中某个顶点v出发,访问v
找出刚访问过的顶点的第一个未被访问的邻接点,访问该顶点。以该顶点为新顶点,重复此步骤,直至刚访问过的顶点没有未被访问的邻接点为止
返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点,访问该顶点
重复步骤(2)和(3),直至图中所有顶点都被访问过,搜索结束
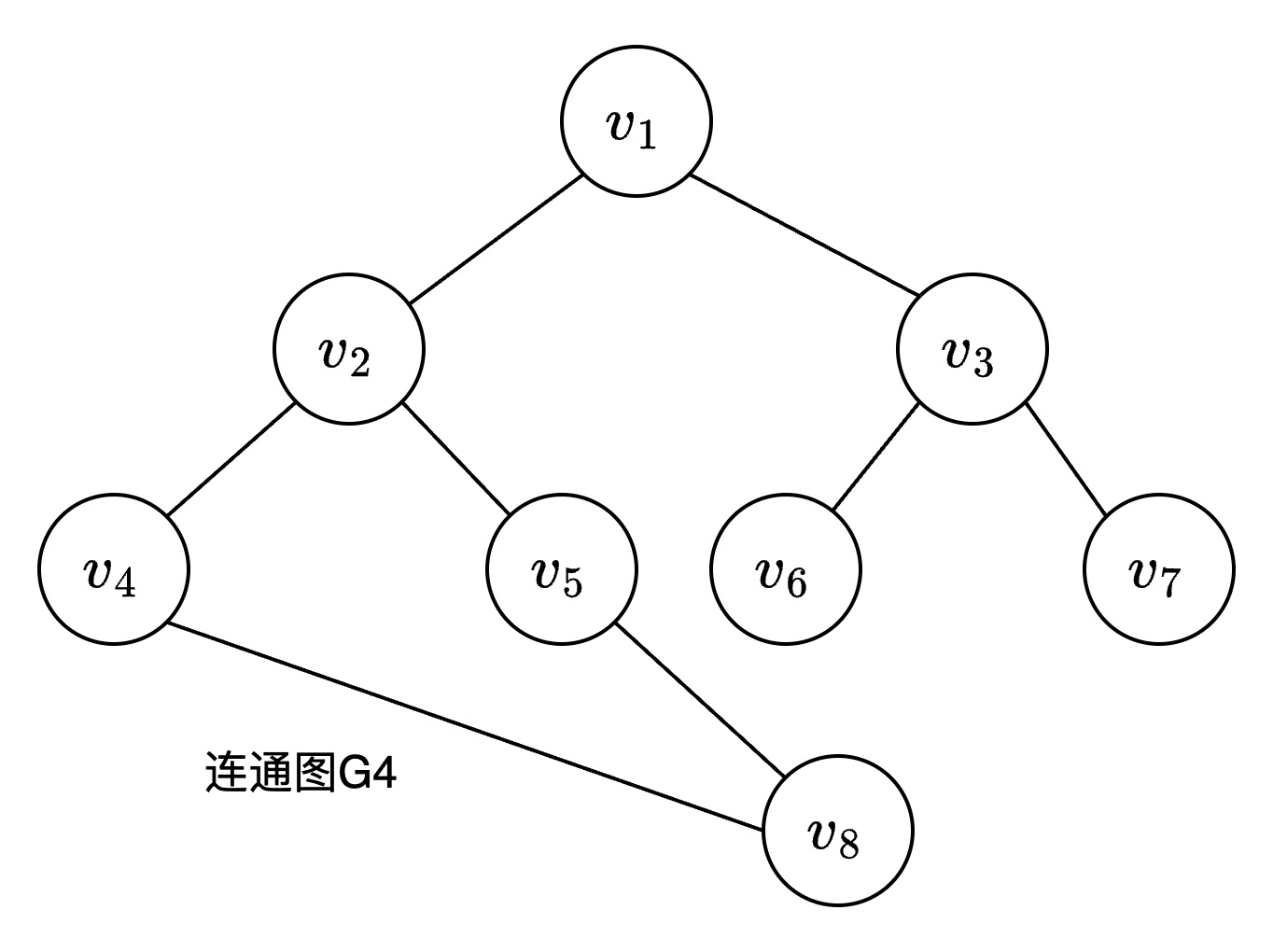
对于连通图G4, 遍历路径\(v_1 -> v_2 ->
v_4 -> v_8 -> v_5 -> v_3 -> v_6 -> v_7\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <stdio.h> #include <stdlib.h> #define MVNum 100 typedef enum {typedef char VerTexType; typedef int ArcType; typedef struct OtherInfo {}OtherInfo; typedef struct ArcNode { int adjvex; struct ArcNode *nextarc ; OtherInfo into; }ArcNode; typedef struct VNode { VerTexType data; ArcNode *firstarc; VisitIf mark; }VNode, AdjList[MVNum]; typedef struct ALGraph { AdjList vertices; int vexnum, arcnum; }ALGraph; void ALGraphDFS (ALGraph *g, int v) { printf ("visited %d\n" , v); g->vertices[v].mark = visited; ArcNode *p = g->vertices[v].firstarc; while (p != NULL ) { if (g->vertices[p->adjvex].mark == unvisited) { ALGraphDFS(g, p->adjvex); } p = p->nextarc; } } void ALGraphDFSTraverse (ALGraph *g) { for (int v = 0 ; v < g->vexnum; v++) { if (g->vertices[v].mark == unvisited) { ALGraphDFS(g, p->adjvex); } } }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 #include <stdio.h> #include <stdlib.h> #define MAX_VERTICES 100 typedef enum {typedef struct Node { int vertex; struct Node * next ; VisitIf mark; } Node; typedef struct Graph { int numVertices; Node* adjLists[MAX_VERTICES]; } Graph; Graph* createGraph (int vertices) { Graph* graph = malloc (sizeof (Graph)); graph->numVertices = vertices; for (int i = 0 ; i < vertices; i++) { graph->adjLists[i] = NULL ; } return graph; } Node* createNode (int v) { Node* newNode = malloc (sizeof (Node)); newNode->vertex = v; newNode->next = NULL ; return newNode; } void addEdge (Graph* graph, int src, int dest) { Node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; } int FirstAdjVex (Graph* graph, int vertex) { Node* adjList = graph->adjLists[vertex]; if (adjList != NULL ) { return adjList->vertex; } return -1 ; } int NextAdjVex (Graph* graph, int vertex, int current) { Node* adjList = graph->adjLists[vertex]; while (adjList != NULL ) { if (adjList->vertex == current) { if (adjList->next != NULL ) { return adjList->next->vertex; } else { return -1 ; } } adjList = adjList->next; } return -1 ; } void DFS (Graph* graph, int vertex, int * visited) { visited[vertex] = 1 ; printf ("Visited %d\n" , vertex); int adjVertex = FirstAdjVex(graph, vertex); while (adjVertex != -1 ) { if (!visited[adjVertex]) { DFS(graph, adjVertex, visited); } adjVertex = NextAdjVex(graph, vertex, adjVertex); } } void printGraph (Graph* graph) { for (int v = 0 ; v < graph->numVertices; v++) { Node* temp = graph->adjLists[v]; printf ("Vertex %d: " , v); while (temp) { printf ("%d -> " , temp->vertex); temp = temp->next; } printf ("NULL\n" ); } } int main () { Graph* graph = createGraph(5 ); addEdge(graph, 0 , 1 ); addEdge(graph, 0 , 4 ); addEdge(graph, 1 , 2 ); addEdge(graph, 1 , 3 ); addEdge(graph, 1 , 4 ); addEdge(graph, 2 , 3 ); addEdge(graph, 3 , 4 ); printGraph(graph); int visited[MAX_VERTICES] = {0 }; printf ("Depth First Search starting from vertex 0:\n" ); DFS(graph, 0 , visited); return 0 ; }
广度优先搜索
类似于树的按层序遍历
遍历过程如下:
从图中某个顶点v出发,访问v
依次访问v的各个未曾访问过的邻接点
分别从这些邻接点出发依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。重复步骤(3),直至图中所有已被访问的顶点的邻接点都被访问到
对于连通图G4, 遍历路径\(v_1 -> v_2 ->
v_3 -> v_4 -> v_5 -> v_6 -> v_7 -> v_7\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 #include <stdio.h> #include <stdlib.h> #define MAX_VERTICES 100 typedef struct Node { int vertex; struct Node * next ; } Node; typedef struct Graph { int numVertices; Node* adjLists[MAX_VERTICES]; } Graph; typedef struct QNode QNode ;typedef struct QNode * QPtr ;struct QNode { int data; struct QNode * next ; }; typedef struct LinkQueue LinkQueue ;struct LinkQueue { QPtr front; QPtr rear; }; void InitQueue (LinkQueue *q) { QPtr node = (QPtr)malloc (sizeof (QNode)); node->next = NULL ; q->front = node; q->rear = node; } void EnQueue (LinkQueue *q, int e) { QPtr p = (QPtr)malloc (sizeof (QNode)); p->data = e; p->next = NULL ; q->rear->next = p; q->rear = p; } void DeQueue (LinkQueue *q, int *e) { if (q->rear == q->front) { return ; } QPtr p = q->front->next; *e = p->data; q->front->next = p->next; if (q->rear == p) { q->rear = q->front; } free (p); } Graph* createGraph (int vertices) { Graph* graph = malloc (sizeof (Graph)); graph->numVertices = vertices; for (int i = 0 ; i < vertices; i++) { graph->adjLists[i] = NULL ; } return graph; } Node* createNode (int v) { Node* newNode = malloc (sizeof (Node)); newNode->vertex = v; newNode->next = NULL ; return newNode; } void addEdge (Graph* graph, int src, int dest) { Node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; } int FirstAdjVex (Graph* graph, int vertex) { Node* adjList = graph->adjLists[vertex]; if (adjList != NULL ) { return adjList->vertex; } return -1 ; } int NextAdjVex (Graph* graph, int vertex, int current) { Node* adjList = graph->adjLists[vertex]; while (adjList != NULL ) { if (adjList->vertex == current) { if (adjList->next != NULL ) { return adjList->next->vertex; } else { return -1 ; } } adjList = adjList->next; } return -1 ; } void BFS (Graph* graph, int vertex, int * visited) { visited[vertex] = 1 ; printf ("Visited %d\n" , vertex); LinkQueue *queue = (LinkQueue*)malloc (sizeof (LinkQueue)); InitQueue(queue ); EnQueue(queue , vertex); while (queue ->rear != queue ->front) { DeQueue(queue , vertex); int adjVertex = FirstAdjVex(graph, vertex); while (adjVertex != -1 ) { if (!visited[adjVertex]) { visited[adjVertex] = 1 ; printf ("Visited %d\n" , adjVertex); EnQueue(queue , adjVertex); } adjVertex = NextAdjVex(graph, vertex, adjVertex); } } } void printGraph (Graph* graph) { for (int v = 0 ; v < graph->numVertices; v++) { Node* temp = graph->adjLists[v]; printf ("Vertex %d: " , v); while (temp) { printf ("%d -> " , temp->vertex); temp = temp->next; } printf ("NULL\n" ); } } int main () { Graph* graph = createGraph(5 ); addEdge(graph, 0 , 1 ); addEdge(graph, 0 , 4 ); addEdge(graph, 1 , 2 ); addEdge(graph, 1 , 3 ); addEdge(graph, 1 , 4 ); addEdge(graph, 2 , 3 ); addEdge(graph, 3 , 4 ); printGraph(graph); int visited[MAX_VERTICES] = {0 }; printf ("Depth First Search starting from vertex 0:\n" ); DFS(graph, 0 , visited); return 0 ; }
图的应用
最小生成树
MST性质: \(u \in U, v \in
V-U\) ,则必定存在一棵包含边(u, v)的最小生成树
普里姆算法
时间复杂度为O(n2),与网中的边数无关,因此适用于求稠密网的最小生成树
构造过程
假设N=(V, E)是连通网,TE是N上最小生成树中边的集合
\(U=\{ u_0 \} (u_0 \in V), \quad TE =
\{\}\) 在所有\(u \in U, \quad v \in
V-U\) 的边\((u, v) \in E\)
中找一条权值最小的边 \((u_0, v_0)\)
并入集合TE,同时 \(v_0\) 并入U
重复步骤2,直到U=V为止 此时TE中必有n-1条边,则T=(V,
TE)为N的最小生成树
算法实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 #define MaxInt 32767 #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct { VerTexType vexs[MVNum]; ArcType arcs[MVNum][MVNum]; int vexnum, arcnum; }AMGraph; struct { VerTexType adjvex; ArcType lowcost; }closedge[MVNum]; int LocateVex (AMGraph *g, VerTexType v) { for (int i = 0 ; i < g->vexnum; i++) { if (g->vexs[i] == v) { return i; } } return -1 ; } int Min () { int min = 10000 ; int k = 0 ; for (int i = 0 ; i < MVNum; i++) { if (closedge[i].lowcost != 0 && closedge[i].lowcost < min) { min = closedge[i].lowcost; k = i; } } return k; } void MiniSpanTree (AMGraph *g, VerTexType u) { int k = LocateVex(g, u); for (int i = 0 ; i < g->vexnum; i++) { if (i != k) { closedge[i].adjvex = u; closedge[i].lowcost = g->arcs[k][i]; } } closedge[k].lowcost = 0 ; for (int i = 1 ; i < g->vexnum; i++) { int k = Min(); VerTexType u0 = closedge[k].adjvex; VerTexType v0 = g->vexs[k]; printf ("%c\t%c\n" , v0, u0); closedge[k].lowcost = 0 ; for (int j = 0 ; j < g->vexnum; j++) { if (g->arcs[k][j] < closedge[j].lowcost) { closedge[j].adjvex = g->vexs[k]; closedge[j].lowcost = g->arcs[k][j]; } } } }
克鲁斯卡尔算法
时间复杂度为O(elog2e),与网中的边数有关,与普里姆算法相比,克鲁斯卡尔算法更适合于求稀疏网的最小生成树
构造过程
假设连通网N=(V, E),将N中的边按权值从小到大的顺序排列
初始状态为只有n个顶点而无边的非连通图T=(V,
{}),图中每个顶点自成一个连通分量
在E中选择权值最小的边,若该边依附的顶点落在T中不同的连通分量上(即不形成回路),则将此边加入到T中,否则舍去此边而选择下一条权值最小的边
重复步骤2,直至T中所有顶点都在同一连通分量上为止
算法实现
结构体Edge:存储边的信息,包括边的两个顶点信息和权值
Vexset[i]:标识各个顶点所属的连通分量。对每个顶点vi∈V,在辅助数组中存在一个相应元素Vexset[i]表示该顶点所在的连通分量。初始时Vexset[i]=i,表示各顶点自成一个连通分量
将数组edges中的元素按权值从小到大排序
依次查看数组edges的边,循环执行以下操作
依次从排好序的数组edges中选出一条边\((U_1,
U_2)\)
在Vexset中分别查找\(v_1\) 和\(v_2\) 所在的连通分量\(vs_1\) 和\(vs_2\) ,进行判断
如果\(vs_1\) 和\(vs_2\) 不等,表明所选的两个顶点分属不同的连通分量,输出此边,并合并\(vs_1\) 和\(vs_2\) 两个连通分量
如果\(vs_1\) 和\(vs_2\) 相等,表明所选的两个顶点属于同一个连通分量,舍去此边而选择下一条权值最小的边
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 #include <stdlib.h> #define MaxInt 32767 #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct { VerTexType vexs[MVNum]; ArcType arcs[MVNum][MVNum]; int vexnum, arcnum; }AMGraph; typedef struct { VerTexType head; VerTexType tail; ArcType lowcost; }Edge; int Vexset[MVNum];int LocateVex (AMGraph *g, VerTexType v) { for (int i = 0 ; i < g->vexnum; i++) { if (g->vexs[i] == v) { return i; } } return -1 ; } int compare (const void *a, const void *b) { Edge *edgeA = (Edge *)a; Edge *edgeB = (Edge *)b; return edgeA->lowcost - edgeB->lowcost; } void MiniSpanTree (AMGraph *g, VerTexType u) { Edge edges[g->vexnum]; int edgeCount = 0 ; for (int i = 0 ; i < g->vexnum; i++) { for (int j = i + 1 ; j < g->vexnum; j++) { if (g->arcs[i][j] != MaxInt) { edges[edgeCount].head = i; edges[edgeCount].tail = j; edges[edgeCount].lowcost = g->arcs[i][j]; edgeCount++; } } } qsort(edges, edgeCount, sizeof (edges[0 ]), compare); for (int i = 0 ; i < g->vexnum; i++) { Vexset[i] = i; } for (int i = 0 ; i < g->arcnum; i++) { int v1 = LocateVex(g, edges[i].head); int v2 = LocateVex(g, edges[i].tail); int vs1 = Vexset[v1]; int vs2 = Vexset[v2]; if (vs1 != vs2) { printf ("%d\t%d\n" , edges[i].head, edges[i].tail); for (int j = 0 ; j < g->vexnum; j++) { if (Vexset[j] == vs2) { Vexset[j] == vs1; } } } } }
最短路径
从某个源点到其余各顶点的最短路径
给定带权有向图G和源点\(v_0\) ,求从\(v_0\) 到G中其余各顶点的最短路径
Dijkstra算法
求解过程
对于网N=(V,E),将N中顶点分成两组:
第一组S:已求出的最短路径的终点集合(初始时只包含源点\(v_0\) )
第二组V-S:尚未求出的最短路径的集合(初始时为V-{\(v_0\) })
算法将按各顶点与\(v_0\) 间最短路径长度递增的次序,逐个将集合V-S中的顶点加入到集合S中去。在这个过程中,总保持\(v_0\) 到集合S中各顶点的路径长度始终不大于到集合V-S中各顶点的路径长度
算法实现
假设用带权的邻接矩阵arcs来表示带权有向网G,G.arcs[i][j]表示弧\(<v_i, v_j>\) 上的权值。若\(<v_i,
v_j>\) 不存在,则置G.arcs[i][j]为\(\infty\) ,源点为\(v_0\)
算法的实现引入以下辅助数组的数据结构:
一维数组S[i]:记录从源点\(v_0\) 到终点\(v_i\) 是否已被确定为最短路径长度,true表示确定,
false表示尚未确定
一维数组Path[i]:记录从源点\(v_0\) 到终点\(v_i\) 的当前最短路径上\(v_i\) 的直接前驱顶点序号。其初值为:如果从\(v_0\) 到\(v_i\) 有弧,则Path[i]为\(v_0\) ,否则为-1
一维数组D[i]:记录从源点\(v_0\) 到终点\(v_i\) 的当前最短路径长度。其初值为:其初值为:如果从\(v_0\) 到\(v_i\) 有弧,则D[i]为弧上的权值,否则为\(\infty\)
步骤如下
初始化:
将源点\(v_0\) 加到S中,即S[\(v_0\) ]=true;
将\(v_0\) 到各个终点的最短路径长度初始为权值,即D[i]=G.arcs[\(v_0\) ][\(v_i\) ], (\(v_i
\in V-S\) )
如果\(v_0\) 和顶点\(v_i\) 之间有弧,则将\(v_i\) 的前驱值为\(v_0\) ,即Path[i]=\(v_0\) ,否则Path[i]=-1
循环n-1次,执行以下操作:
选择下一条最短路径的终点\(v_k\) ,使得:\(D[k] = Min\{D[i] \quad | \quad v_i \in
V-S\}\)
将\(v_k\) 加到S中,即S[\(v_k\) ]=true
根据条件更新从\(v_0\) 出发到集合V-S上任一顶点的最短路径的长度。若条件D[k]+G.arcs[k][i]
< D[i]成立,则更新D[i]=D[k]+G.arcs[k][i],同时更改\(v_i\) 的前驱为\(v_k\) ,Paht[i]=k
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 #define MaxInt 32767 #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct { VerTexType vexs[MVNum]; ArcType arcs[MVNum][MVNum]; int vexnum, arcnum; }AMGraph; void ShortestPath (AMGraph *g, int v0) { int s[g->vexnum]; int path[g->vexnum]; int d[g->vexnum]; int n = g->vexnum; for (int v = 0 ; v < n; v++) { s[v] = 0 ; d[v] = g->arcs[v0][v]; if (d[v] < MaxInt) { path[v] = v0; } else { path[v] = -1 ; } } s[v0] = 1 ; d[v0] = 0 ; for (int i = 1 ; i < n; i++) { int v = 0 ; int min = MaxInt; for (int w = 0 ; w < n; w++) { if (s[w] == 0 && d[w] < min) { v = w; min = d[w]; } } s[v] = 1 ; for (int w = 0 ; w < n; w++) { if (s[w] == 0 && d[v] + g->arcs[v][w] < d[w]) { d[w] = d[v] + g->arcs[v][w]; path[w] = v; } } } }
每一对顶点之间的最短路径
Floyd算法 \(v_i\) 到\(v_j\) 的最短路径
算法实现
辅助数据结构
二维数组Path[i][j]:最短路径上顶点\(v_j\) 的前一顶点的序号
二维数组D[i][j]:记录顶点\(v_i\) 和顶点\(v_j\) 之间的最短路径长度
步骤如下
将\(v_i\) 到\(v_j\) 的最短路径长度初始化,即D[i][j]=G.arcs[i][j],然后进行n次比较和更新
在\(v_i\) 和\(v_j\) 间加入顶点\(v_0\) ,比较\((v_i, v_j)\) 和\((v_i, v_0,
v_j)\) 的路径长度,取其中较短者作为\(v_i\) 到\(v_j\) 的中间顶点序号不大于0的最短路径
在\(v_i\) 和\(v_j\) 间加入\(v_1\) , 得到\((v_j, \cdots, v_1)\) 和\((v_1, \cdots, v_j)\) ,其中\((v_j, \cdots, v_1)\) 是\(v_j\) 到\(v_1\) 的且中间顶点的序号不大于0的最短路径,\((v_1, \cdots, v_j)\) 是\(v_1\) 到\(v_j\) 的且中间顶点序号不大于0的最短路径,这两条路径已在上一步中求出。比较\((v_i, \cdots, v_1, \cdots,
v_j)\) 与上一步求出的\(v_i\) 到\(v_j\) 的中间顶点序号不大于0的最短路径,取其中较短者作为\(v_i\) 到\(v_j\) 的中间顶点序号不大于1的最短路径
依此类推,在\(v_i\) 和\(v_j\) 间加入顶点\(v_k\) ,若\((v_i,
\cdots, v_k)\) 和\((v_k, \cdots,
v_j)\) 分别是\(v_i\) 到\(v_k\) 和\(v_k\) 到\(v_j\) 的中间顶点序号不大于k-1的最短路径,则将\((v_i, \cdots, v_k, \cdots,
v_j)\) 和已经得到的从\(v_i\) 到\(v_j\) 且中间顶点序号不大于k-1的最短路径相比较,其长度较短者便是从\(v_i\) 到\(v_j\) 的中间顶点序号不大于k的最短路径。这样,经过n次比较后,最后求得的必是从\(v_i\) 到\(v_j\) 的最短路径
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #define MaxInt 32767 #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct { VerTexType vexs[MVNum]; ArcType arcs[MVNum][MVNum]; int vexnum, arcnum; }AMGraph; void ShortestPath (AMGraph *g) { int path[MVNum][MVNum]; int d[MVNum][MVNum]; for (int i = 0 ; i < g->vexnum; i++) { for (int j = 0 ; j < g->vexnum; j++) { d[i][j] = g->arcs[i][j]; if (d[i][j] < MaxInt) { path[i][j] = i; } else { path[i][j] = -1 ; } } for (int k = 0 ; k < g->vexnum; g++) { for (int i = 0 ; i < g->vexnum; i++) { for (int j = 0 ; j < g->vexnum; j++) { if (d[i][k] + d[k][j] < d[i][j]) { d[i][j] = d[i][k] + d[k][j]; path[i][j] = path[k][j]; } } } } } }
拓扑排序
拓扑排序过程
在有向图中选一个无前驱的顶点且输出它
从图中删除该顶点和所有以它为尾的弧
重复1和2,直至不存在无前驱的顶点
若此时输出的顶点数小于有向图中的顶点数,则说明有向图中有环,否则输出的顶点序列即为一个拓扑序列
拓扑排序实现
辅助数据结构
一维数组indegree[i]:存放各顶点入度,没有前驱的顶点就是入度为零的顶点。删除顶点及以它为尾的弧的操作,可不必真正为图的存储结构进行改变,可用弧头顶点的入度减1的办法来实现
栈s:暂存所有入度为零的顶点,这样可以避免重复扫描数组indegree检测入度为零的顶点,提高算法效率
一维数组topo[i]:记录拓扑序列的顶点序号
算法步骤
求出各顶点的入度存入数组indegree[i]中,并将入度为零的顶点入栈
只要栈不空,则重复以下操作:
将栈顶顶点\(v_i\) 出栈并保存在拓扑数组topo中
对顶点\(v_i\) 的每个邻接点\(v_k\) 的入度减1,如果\(v_k\) 的入度变为0,则将\(v_k\) 入栈
如果输出顶点个数少于AOV-网的顶点个数,则网中存在环,无法进行拓扑排序,否则拓扑排序成功
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 #include <stdio.h> #include <stdlib.h> #define MVNum 100 typedef char VerTexType; typedef int ArcType; typedef struct ArcNode { int adjvex; struct ArcNode *nextarc ; }ArcNode; typedef struct VNode { VerTexType data; ArcNode *firstarc; }VNode, AdjList[MVNum]; typedef struct ALGraph { AdjList vertices; int vexnum, arcnum; }ALGraph; typedef struct StackNode { int data; struct StackNode * next ; }StackNode,*LinkStack; int InitStack (LinkStack s) { s = NULL ; return 0 ; } LinkStack Push (LinkStack s, int e) { LinkStack p = (LinkStack)malloc (sizeof (StackNode)); p->data = e; p->next = s; s = p; return s; } LinkStack Pop (LinkStack s, int *e) { if (s == NULL ) { return s; } *e = s->data; LinkStack p = s; s = s->next; free (p); return s; } void FindInDegree (ALGraph *g, int indegree[]) { for (int i = 0 ; i < g->vexnum; i++) { indegree[i] = 0 ; } for (int i = 0 ; i < g->vexnum; i++) { ArcNode *p = g->vertices[i].firstarc; while (p) { indegree[p->adjvex]++; p = p->nextarc; } } } int TopologicalSort (ALGraph *g, int topo[]) { int indegree[MVNum]; FindInDegree(g, indegree); LinkStack s; InitStack(s); for (int i = 0 ; i < g->vexnum; i++) { if (indegree[i] == 0 ) { Push(s, i); } } int m = 0 ; while (s != NULL ) { int i; Pop(s, &i); topo[m++] = i; ArcNode *p = g->vertices[i].firstarc; while (p != NULL ) { int k = p->adjvex; --indegree[k]; if (indegree[k] == 0 ) { Push(s, k); } p = p->nextarc; } } if (m < g->vexnum) { return 0 ; } return 1 ; }
关键路径
求解过程
对图中顶点进行排序,在排序过程中按拓扑序列求出每个事件的最早发生时间ve(i)
按逆拓扑序列求出每个事件的最迟发生时间vl(i)
求出每个活动\(a_i\) 的最早开始时间e(i)
求出每个活动\(a_i\) 的最晚开始时间l(i)
找出e(i)=l(i)的活动\(a_i\) ,即位关键活动。由关键活动形成的由源点到汇点的每一条路径就是关键路径,关键路径有可能不止一条
算法实现
由于每个事件的最早发生时间ve(i)和最迟发生时间vl(i)要在拓扑序列的基础上进行计算,所以关键路径算法的实现要基于拓扑排序算法,采用邻接表做有向图的存储结构
辅助数据结构
一维数组ve[i]:事件\(v_i\) 的最早发生时间
一维数组vl[i]:事件\(v_i\) 的最迟发生时间
一维数组topo[i]:记录拓扑序列的顶点序号
算法步骤
调用拓扑排序算法,使拓扑序列保存在数组topo中
将每个事件的最早发生时间ve[i]初始化为零
根据topo中的值,按从前向后的拓扑次序,依次求每个事件的最早发生时间,循环几次,执行以下操作:
取得拓扑序列中的顶点序号k,k=topo[i]
用指针p依次指向k的每个邻接顶点,取得每个邻接顶点的序号j=p->adjvex,依次更新顶点j的最早发生时间ve[j]
\(if (ve[j] < ve[k]+p->weight) ve[j] =
ve[k] + p->weight;\)
将每个事件的最迟发生时间vl[i]初始化为汇点的最早发生时间,
vl[i]=ve[n-1]
根据topo中的值,按从后向前的逆拓扑次序,依次求每个时间的最迟发生时间,循环n次,执行以下操作:
取得拓扑序列中的顶点序号k,k=topo[i]
用指针p依次指向k的每个邻接顶点,取得每个邻接顶点的序号j=p->adjvex,依次根据k的邻接点,更新k的最迟发生时间vl[k]
\(if (vl[k] > vl[j] - p->weight) vl[k] =
vl[j] - p->weight\)
判断某一活动是否为关键活动,循环n次,执行以下操作:对于每个顶点i,用指针p依次指向i的每个邻接点,取得每个邻接顶点的序号j=p->adjvex,分别计算活动<\(v_i\) , \(v_j\) >的最早和最迟发生时间e和l,e=ve[i];l=vl[j]-p->weight;。如果e和l相等,则活动<\(v_i\) , \(v_j\) >为关键活动,输出弧\(v_j\)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 #include <stdio.h> #include <stdlib.h> #define MVNum 100 typedef char VerTexType; typedef struct ArcNode { int adjvex; int weight; struct ArcNode *nextarc ; }ArcNode; typedef struct VNode { VerTexType data; ArcNode *firstarc; }VNode, AdjList[MVNum]; typedef struct ALGraph { AdjList vertices; int vexnum, arcnum; }ALGraph; typedef struct StackNode { int data; struct StackNode * next ; }StackNode,*LinkStack; int InitStack (LinkStack s) { s = NULL ; return 0 ; } LinkStack Push (LinkStack s, int e) { LinkStack p = (LinkStack)malloc (sizeof (StackNode)); p->data = e; p->next = s; s = p; return s; } LinkStack Pop (LinkStack s, int *e) { if (s == NULL ) { return s; } *e = s->data; LinkStack p = s; s = s->next; free (p); return s; } void FindInDegree (ALGraph *g, int indegree[]) { for (int i = 0 ; i < g->vexnum; i++) { indegree[i] = 0 ; } for (int i = 0 ; i < g->vexnum; i++) { ArcNode *p = g->vertices[i].firstarc; while (p) { indegree[p->adjvex]++; p = p->nextarc; } } } int TopologicalSort (ALGraph *g, int topo[]) { int indegree[MVNum]; FindInDegree(g, indegree); LinkStack s; InitStack(s); for (int i = 0 ; i < g->vexnum; i++) { if (indegree[i] == 0 ) { Push(s, i); } } int m = 0 ; while (s != NULL ) { int i; Pop(s, &i); topo[m++] = i; ArcNode *p = g->vertices[i].firstarc; while (p != NULL ) { int k = p->adjvex; --indegree[k]; if (indegree[k] == 0 ) { Push(s, k); } p = p->nextarc; } } if (m < g->vexnum) { return 0 ; } return 1 ; } int CriticalPath (ALGraph *g) { int topo[g->vexnum]; int ve[g->vexnum]; int vl[g->vexnum]; if (TopologicalSort(g, topo) == 0 ) { return 0 ; } for (int i = 0 ; i < g->vexnum; i++) { ve[i] = 0 ; } for (int i = 0 ; i < g->vexnum; i++) { int k = topo[i]; ArcNode *p = g->vertices[k].firstarc; while (p != NULL ) { int j = p->adjvex; if (ve[j] < ve[k] + p->weight) { ve[j] = ve[k] + p->weight; } p = p->nextarc; } } for (int i = 0 ; i < g->vexnum; i++) { vl[i] = ve[g->vexnum-1 ]; } for (int i = g->vexnum-1 ; i >= 0 ; i--) { int k = topo[i]; ArcNode *p = g->vertices[k].firstarc; while (p != NULL ) { int j = p->adjvex; if (vl[k] > vl[j] - p->weight) { vl[k] = vl[j] - p->weight; } p = p->nextarc; } } for (int i = 0 ; i < g->vexnum; i++) { ArcNode *p = g->vertices[i].firstarc; while (p != NULL ) { int j = p->adjvex; int e = ve[i]; int l = vl[j] - p->weight; if (e == l) { printf ("关键活动: %c -> %c\n" , g->vertices[i].data, g->vertices[j].data); } p = p->nextarc; } } }
 若G是网,则邻接矩阵可以定义为
若G是网,则邻接矩阵可以定义为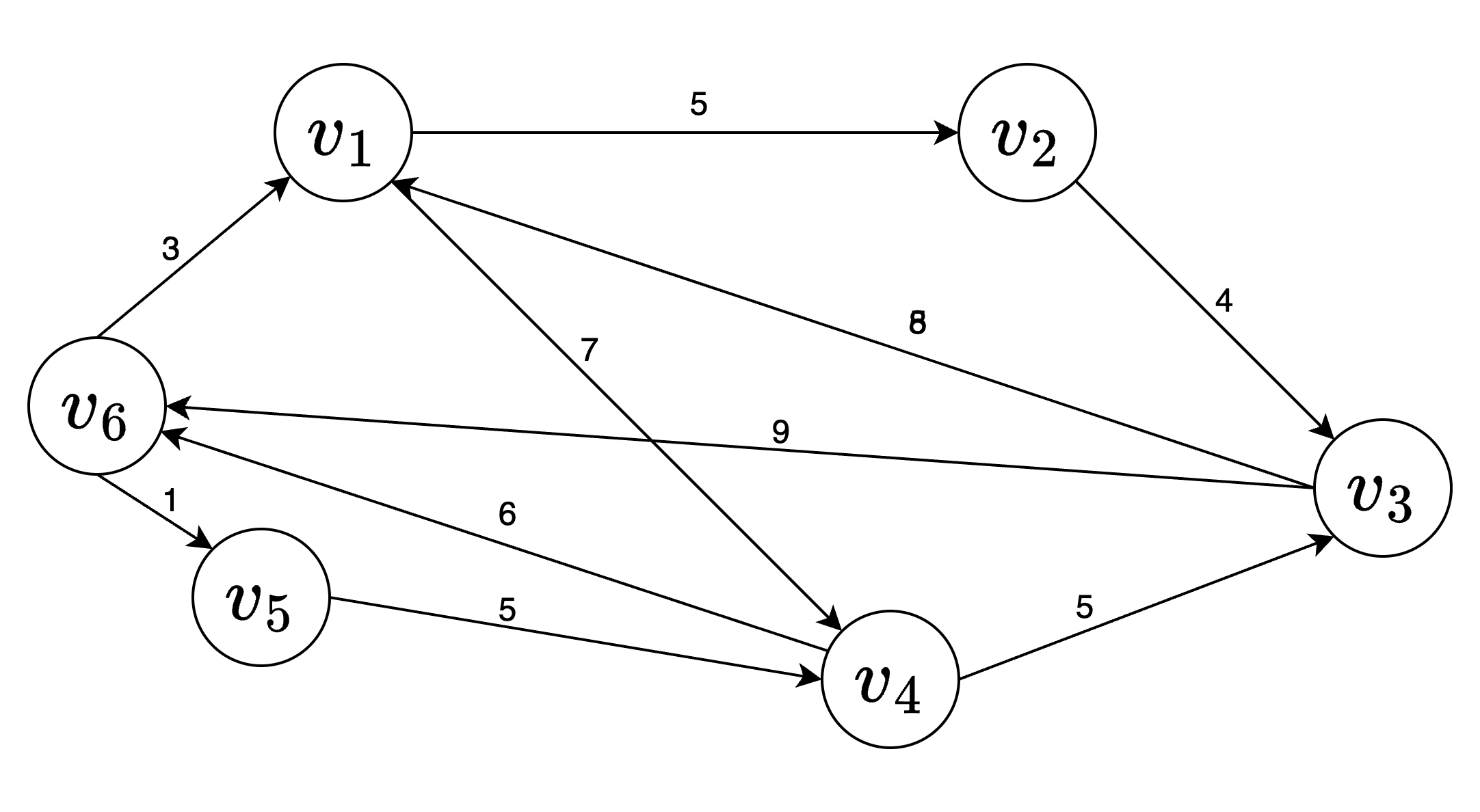 创建无向网 时间复杂度\(O(n^2)\)
创建无向网 时间复杂度\(O(n^2)\) * 无向图的邻接表中,顶点\(v_i\)的度恰为第
* 无向图的邻接表中,顶点\(v_i\)的度恰为第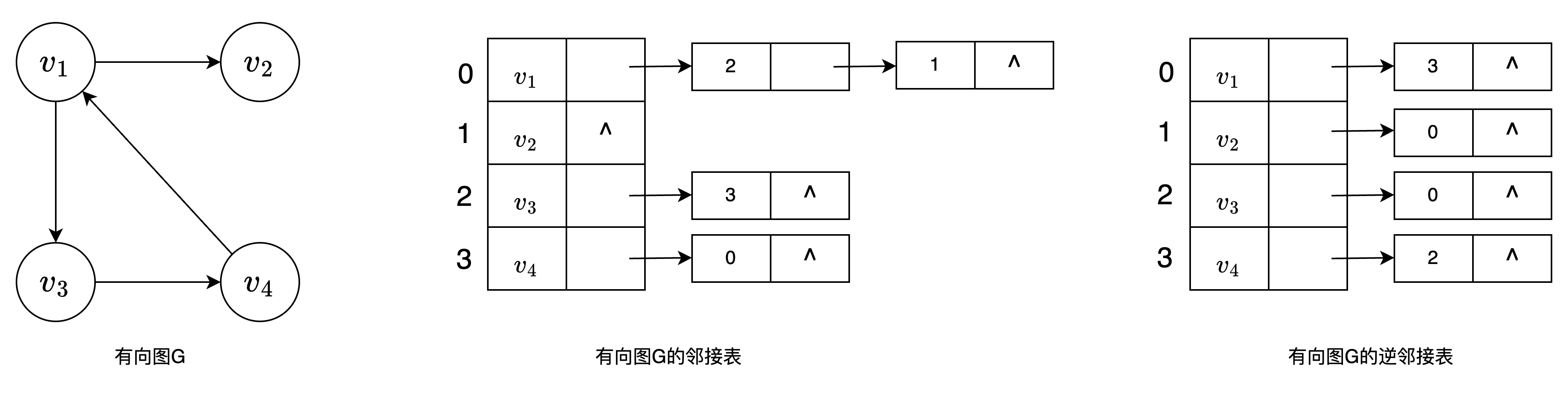

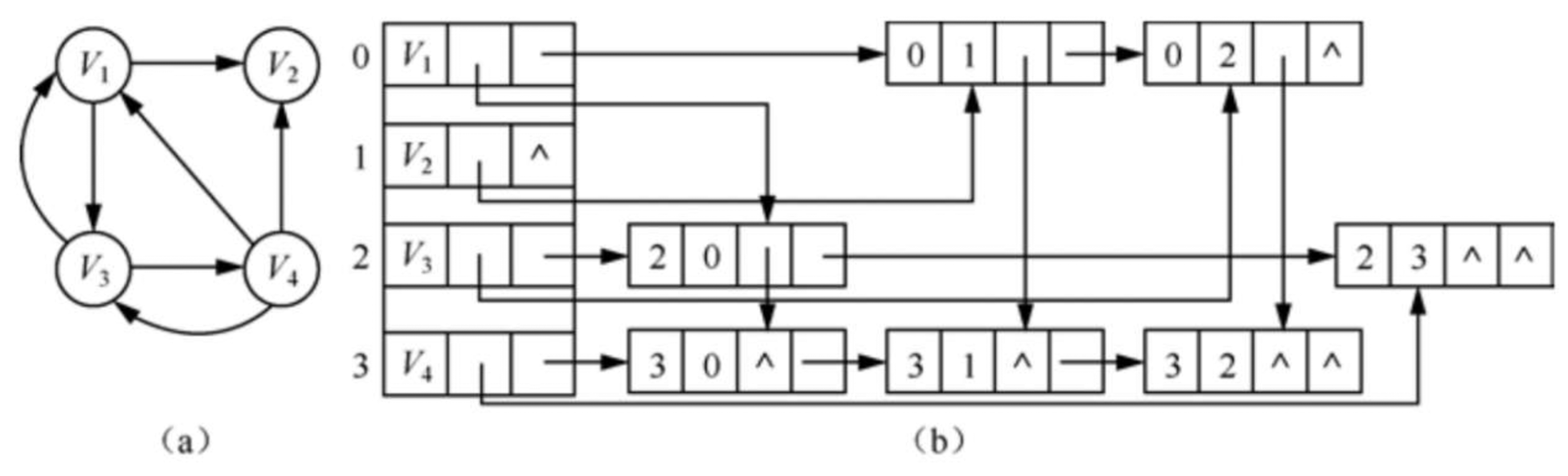 若将有向图的邻接矩阵看成稀疏矩阵的话,则十字链表也可以看成是邻接矩阵的链式存储结构,在图的十字链表中,弧结点所在的链表非循环链表,结点之间相对位置自然形成,不一定按照顶点序号有序,表头结点即顶点结点,它们之间不是链接,而是顺序存储。
若将有向图的邻接矩阵看成稀疏矩阵的话,则十字链表也可以看成是邻接矩阵的链式存储结构,在图的十字链表中,弧结点所在的链表非循环链表,结点之间相对位置自然形成,不一定按照顶点序号有序,表头结点即顶点结点,它们之间不是链接,而是顺序存储。
 对于一个连通图,深度优先搜索遍历的过程如下:
对于一个连通图,深度优先搜索遍历的过程如下: