字符串、数组和广义表
#数据结构 #字符串 #数组 #广义表

字符串

字符串一般简称串。串是一种特殊的线性表，其特殊性体现在数据元素是一个字符，也就是说，串是一种内容受限的线性表。

串由 零个或多个字符 组成的有限序列。 由一个或多个空格组成的串称为 空格串

模式匹配算法

自串的定位运算通常称为串的 模式匹配 或者 串匹配 。

BF算法

BF算法思路直观简明。但当匹配失败时，主串的指针j总是回溯到i-j+2位置，模式串的指针总是恢复到首字符位置j=1，因此算法时间复杂度高, 是O(n*m)

  1. 分别利用计数指针i和j指示主串S和模式串T中当前正在比较的字符 位置，i初值为1，j初值为1
  2. 如果两个串均未比较到串尾，即i和j均分别小于等于S和T的长度时，则循环执行以下操作：
    1. S.ch[i]和T.ch[j]比较，若相等，则i和j分别指示串中下个位置，继续比较后续字符
    2. 若不等，指针后退重新开始匹配，从主串的下一个字符(i=i-j+2)起再重新和模式的第一个字符(j=1)比较
  3. 如果j>T.length，说明模式T中的每个字符依次和主串S中的一个连续字符序列相等，则匹配成功。返回和模式T中第一个字符相等的字符在主串S中的序号(i-T.length)；否则成匹配不成功，返回0。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
typedef struct  SString SString;

struct SString
{
    char *ch;
    int length;
};

int BF(SString S, SString T, int pos)
{
    int i = pos;
    int j = 1;
    while (i <= S.length && j <= T.length)
    {
        if (S.ch[i] == T.ch[j])
        {
            ++i;
            ++j;
        }
        else
        {
            i = i - j + 2;
            j = 1;
        }
    }
    if (j > T.length)
    {
        return i - T.length;
    }
    return 0;
}

KMP算法

该算法是BF算法的改进版，可以在O(n+m)的时间数量级上完成串的模式匹配。其改进在于：每当一趟匹配过程中出现字符比较不等时，不需回溯i指针，而是利用已经得到的"部分匹配"的结果将模式向右“滑动”尽可能远的一段距离后，继续进行比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
typedef struct  SString SString;

struct SString
{
    char *ch;
    int length;
};

int KMP(SString s, SString t)
{
    int i = 1;
    int j = 1;
    int next[255];
    build_next(t, next);
    while ( i <= s.length && j <= t.length)
    {
        if (j == 0 || s.ch[i] == t.ch[j])
        {
            ++i;
            ++j;
        }
        else
        {
            j = next[j];
        }
    }
    printf("i: %d, j: %d\n", i, j);
    if (j > t.length)
    {
        return i-t.length;
    }
    return 0;
}

计算next数组

下标从1开始 next[1] = 0 (A) 设next[j]=k,这表明在模式串中存在下列关系:

\[ t_1t_2t_3...t_{k-1} = t_{j-k+1}t_{j-k+2}...t_{j-1} \]

其中k为满足1<k<j的某个值，并且不可能存在k'>k满足等式A。此时next[j+1]=?可能有以下两种情况:

  1. 若\(t_j=t_k\), 则表明在模式串中

\[ t_1t_2t_3...t_{k} = t_{j-k+1}t_{j-k+2}...t_{j} \]

并且不可能存在k'>k满足等式A，这就是说next[j+1]=k+1，即next[j+1]=next[j]+1

  1. 若\(t_j \neq t_k\), 则表明在模式串中

\[ t_1t_2t_3...t_k != t_{j-k+1}t_{j-k+2}...t_j \]

此时可把求next函数值的问题看成是一个模式匹配的问题，整个模式串即是主串也是模式串，而当前在匹配过程中，已有\(t_{j-k+1}=t_1\),\(t_{j-k+2}=t_2\), ...,\(t_{j-1}=t_{k-1}\)，则当\(t_j \neq t_k\)时应将模式向右滑动至以模式中的第next[k]个字符和主串中第j个字符相比较。若next[k]=k',且\(t_j=t_{k'}\)，则说明在主串中第j+1个字符之前存在一个长度为k'（即next[k])的最长自串，和模式串中从首字符其长度为k'的子串相等，即

当(1<k'<k<j)时:

\[ t_1t_2t_3...t_{k'} = t_{j-k'+1}t_{j-k'+2}...t_j \]

这就是说next[j+1]=k'+1, 即

next[j+1] = next[k]+1

同理，若\(t_j \neq t_{k'}\)，则将模式继续向右滑动直至模式中第next[k]个字符和tj对齐 ..., 以此类推，直至tj和模式中某个字符匹配成功或者不存在任何k'(1<k'<j)满足等式A，则next[j+1]=1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// next函数值取决于模式串本身,和相匹配的主串无关.
void build_next(SString t, int *next)
{
    next[1] = 0;
    int i = 1;
    int j = 0;
    while (i < t.length)
    {
        if (j == 0 || t.ch[i] == t.ch[j])
        {
            ++i;
            ++j;
            next[i] = j;
        } else {
            j = next[j];
        }
    }
}

计算next【优化版】

前面定义的next函数尚有缺陷。例如模式串"aaaab"和主串“aaabaaaab"匹配时，当\(i=4, j=4\) 时 \(s.ch[4] \neq t.ch[4]\), 由next[j]的指示还需要进行i=4、j=3, i=4、j=2, i=4、j=1这3次比较。实际上模式中1～3个字符和第4个字符都相等，因此不需要再和主串中第4个字符比较，而可以将模式连续向右滑动4个字符的位置直接进行i=5、j=1的字符比较。这就是说，若表述定义得到的next[j]=k, 而模式中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void build_nextval(SString t, int *next)
{
    next[1] = 0;
    int i = 1;
    int j = 0;
    while (i <= t.length)
    {
        if (j == 0 || t.ch[i] == t.ch[j])
        {
            ++i;
            ++j;
            if (t.ch[i] != t.ch[j])
            {
                next[i] = j;
            } else {
                next[i] = next[j];
            }
        } else {
            j = next[j];
        }
    }
}

数组

数组是由类型相同的数组元素构成的有序集合，每个元素称为数组元素。 数组一旦被定义，它的维数和维界就不再改变，数组一般只有存取元素和修改元素值的操作。

矩阵形式表示 \[ A_{m \times n} = \begin{Bmatrix} a_{00} & a_{01} & a_{02} & \cdots & a_{0,n-1} \\ a_{10} & a_{11} & a_{12} & \cdots & a_{1,n-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m-1,0} & a_{m-1,1} & a_{m-1,2} & \cdots & a_{m-1,n-1} \\ \end{Bmatrix} \]

列向量的一维数组 \[ A_{m \times n } = \begin{Bmatrix} \begin{Bmatrix} a_{00} \\ a_{10} \\ \vdots \\ a_{m-1,0} \end{Bmatrix} \begin{Bmatrix} a_{01} \\ a_{11} \\ \vdots \\ a_{m-1,1} \end{Bmatrix} \begin{Bmatrix} a_{02} \\ a_{12} \\ \vdots \\ a_{m-1,2} \end{Bmatrix} \cdots \begin{Bmatrix} a_{0,n-1} \\ a_{1,n-1} \\ \vdots \\ a_{m-1,n-1} \end{Bmatrix} \end{Bmatrix} \]

行向量的一维数组 \[ A_{m \times n} = ((a_{00}a_{01}\cdots a_{0,n-1}),(a_{10}a_{11}\cdots a_{1,n-1}),\cdots(a_{m-1,0}a_{m-1,1}\cdots a_{m-1,n-1})) \]

数组的存储顺序

由于数组一般不做插入或删除操作，故结构中的数据元素个数和元素之间的关系不再发生变动，因此采用顺序存储结构表示比较合适

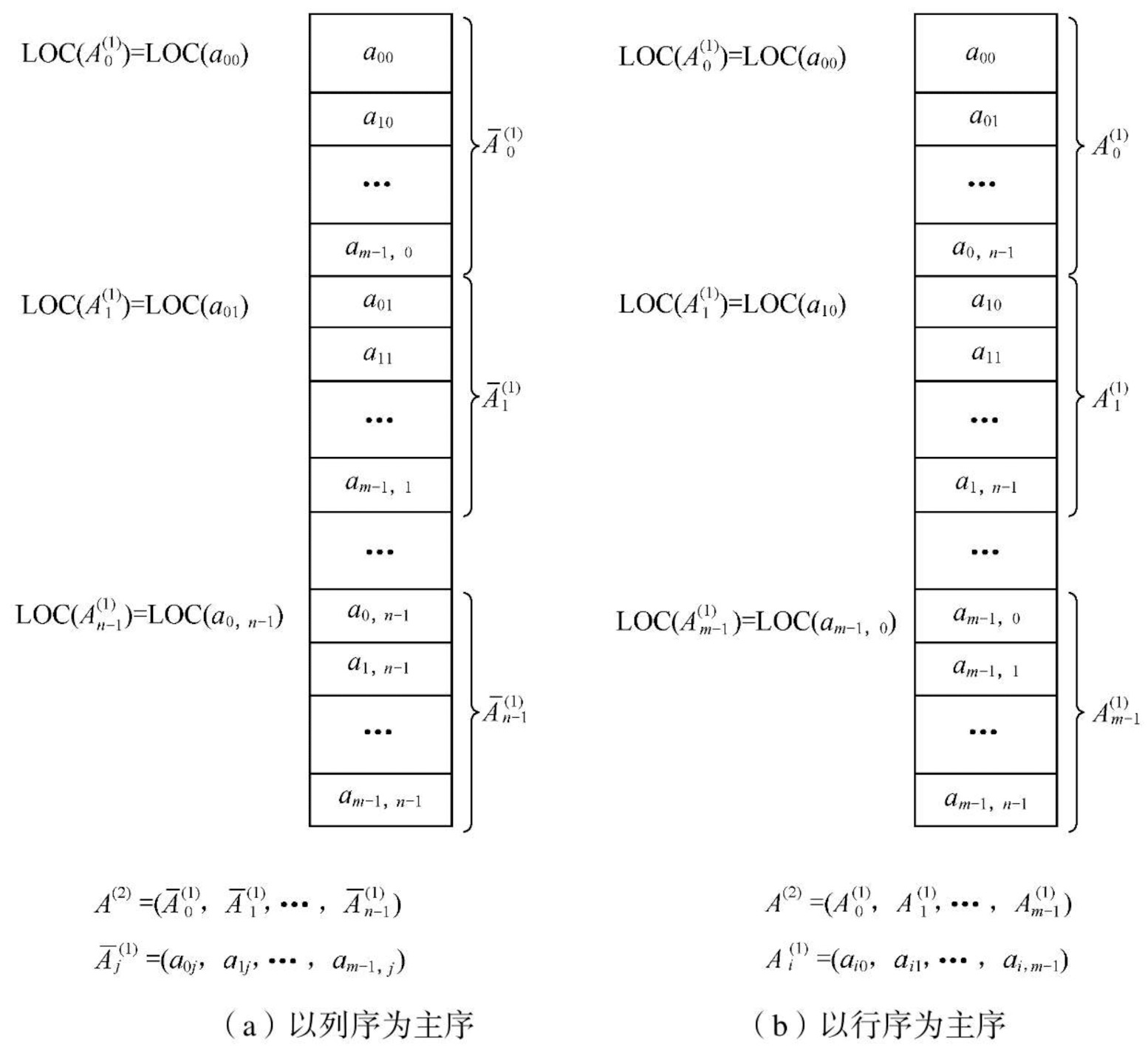数组存储方式.jpg 假设每个数据元素占L个存储单元，则二维数组\(A_{m \times n}\)按行序存储时，任一元素\(a_{ij}\)的存储位置可由下列公式确定

\[ LOC(i,j) = LOC(0,0) + (n \times i + j)L \]

特殊矩阵

对称矩阵

若n阶矩阵A中元素满足下述性质，则称为n阶对称矩阵(\(1 \le i,j \le n\))

\[ a_{ij} = a_{ji} \]

对于对称矩阵，可以为每一对称元素分配应该存储空间，则可将\(n^2\)个元素压缩存储到n(n+1)/2个元素的空间中。假设一维数组A'[n(n+1)/2]作为n阶矩阵A的存储结构，则A'[k]和矩阵元素\(a_{ij}\)之间存在着一一对应的关系

\[ k = \begin{cases} \cfrac{i(i-1)}{2} + j - 1 \quad [if \quad i \ge j] \\ \cfrac{j(j-1)}{2} + i - 1 \quad [if \quad i \lt j] \end{cases} \]

三角矩阵

以对角线划分，三角矩阵有上三角矩阵和下三角矩阵两种。上三角矩阵是指矩阵下三角(不包括对角线)中的元素均为常数c或零的n阶矩阵，下三角与之相反。对三角矩阵进行压缩存储时，除了和对称矩阵一样，只存储其上（下）三角中的元素之外，再加一个常数c的存储空间即可

上三角矩阵

\[ k = \begin{cases} \cfrac{(i-1)(2n-i+2)}{2} + (j-i) \quad [if \quad i \le j] \\ \cfrac{n(n+1)}{2} \quad [if \quad i \gt j] \end{cases} \]

下三角矩阵

\[ k = \begin{cases} \cfrac{i(i-1)}{2} + j - 1 \quad [if \quad i \ge j] \\ \cfrac{n(n+1)}{2} \quad [if \quad i \lt j] \end{cases} \]

广义表

广义表是线性表的推广，也称为列表。广义表的定义是一个递归的定义，它的元素可以是子表，而子表的元素还可以是子表

由于广义表中的数据元素可以有不同的结构（或是原子，或是列表），因此难以用顺序存储结构表示，通常采用链式存储结构。

一对确定的表头和表尾可唯一确定广义表

运算

  1. 取表头：取出的表头为非空广义表的第一个元素，可以是原子，也可以是子表
  2. 取表尾：取出的表尾为除去表头外，由其余元素构成的子表。即表尾一定是广义表

头尾链表的存储结构

由于广义表的数据元素可能是原子或者广义表，由此需要两种结构的结点：

  • 表结点： 表示广义表
  • 原子结点： 表示原子

一个表结点由三个域组成：标识域、指示表头的指针域和指示表尾的指针域，而原子结点只需两个域：标识域和值域。如下所示，tag是标识域，值为1表明结点是子表，值为0表明结点是原子

表结点

tag=1 hp tp

原子结点

tag=1 atom

定义如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 广义表的头尾链表存储表示
// ATOM = 0 原子
// LIST = 1 子表
typedef enum{ATOM, LIST} ElemTag;

typedef struct GLNode
{
    ElemTag tag;
    union
    {
        AtomType atom; // atom时原子结点的值域,AtomType由用户定义
        struct
        {
            struct GLNode* hp, *tp;
        }ptr; // ptr是表结点的指针域，ptr.hp和ptr.tp分别指向表头和表尾
    };
}*GList;
  1. 除空表的表头指针为空外，对任何非空广义表，其表头指针均指向一个表结点，且结点中的hp域指示广义表表头（或为原子结点，或为表结点），tp域指向广义表表尾（除非表尾为空，则指针为空，否则必为表结点）
  2. 容易分清列表中原子和子表所在层次
  3. 最高层的表结点个数即为广义表的长度

扩展线性链表的存储结构

表结点

tag=1 hp tp

原子结点

tag=1 atom tp
上一页
#数据结构 #字符串 #数组 #广义表
下一页